Реферат: Спектральный анализ колебаний
Академия России
Кафедра Физики
Реферат на тему:
СПЕКТРАЛЬНЫЙ АНАЛИЗ КОЛЕБАНИЙ
Орел 2009
Содержание
Введение
Спектральный состав периодических колебаний
Анализ периодических колебаний
Частотный состав непериодического колебания
Библиографический список
Вступление
Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления радиотехнических сигналов, исключительное место занимают гармонические функции. Их значение обусловлено рядом причин, основными из которых являются:
– гармонические сигналы инвариантны (не изменяются) относительно преобразований, осуществляемых стационарными линейными электрическими цепями. Если такая цепь возбуждена источником гармонических колебаний, то сигнал на выходе цепи остается гармоническим с той же частотой, отличаясь от входного сигнала лишь амплитудой и начальной фазой;
– техника генерирования гармонических сигналов достаточно проста.
Кроме того, известно (курс математики), что любое негармоническое колебание, удовлетворяющее определенным условиям, можно представить в виде суммы гармонических колебаний. При этом говорят, что осуществлено спектральное разложение этого сигнала, а отдельные гармонические компоненты сигнала образуют его спектр.
Спектральный состав периодических колебаний
Математической моделью процесса, повторяющегося во времени, является периодическое колебание ![]() со следующим свойством:
со следующим свойством:
![]() , n = 1, 2, …,
, n = 1, 2, …,
где Т – период колебания.
Известно, что любая периодическая функция, удовлетворяющая условиям Дирихле (интервал, на котором функция определена, может быть разбит на конечное число интервалов, в каждом из которых функция непрерывна и монотонна, и во всякой точке разрыва функции существуют переходы от одного конечного значения к другому), может быть представлена рядом Фурье. Если ряд Фурье представлен в тригонометрической форме, то его запись имеет следующий вид:
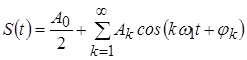 , k = 0, 1, 2, …,
, k = 0, 1, 2, …,
где ![]() .
.
То есть периодическое колебание можно представить как сумму постоянной составляющей ![]() и гармонических колебаний с частотами k w1 (гармоник), причем совокупность амплитуд гармоник
и гармонических колебаний с частотами k w1 (гармоник), причем совокупность амплитуд гармоник ![]() называется спектром амплитуд колебания
называется спектром амплитуд колебания ![]() , а совокупность начальных фаз
, а совокупность начальных фаз ![]() называется спектром фаз колебания
называется спектром фаз колебания ![]() .
.
Очень часто используют комплексную форму ряда Фурье. Для перехода к этой форме воспользуемся формулой Эйлера:
![]() .
.
Тогда ряд Фурье запишется в виде
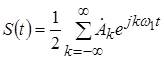 .
.
Отсюда легко определяются комплексные амплитуды гармоник:
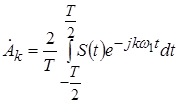 .
.
Поскольку периодическое колебание ![]() известного периода Т полностью описывается совокупностью амплитуд
известного периода Т полностью описывается совокупностью амплитуд ![]() и фаз
и фаз ![]() своих составляющих, то задание спектра такого колебания сводится к заданию его спектров амплитуд и фаз.
своих составляющих, то задание спектра такого колебания сводится к заданию его спектров амплитуд и фаз.
Пример графического изображения спектров амплитуд ![]() и фаз
и фаз ![]() некоторого периодического колебания приведен на рисунке 1.
некоторого периодического колебания приведен на рисунке 1.
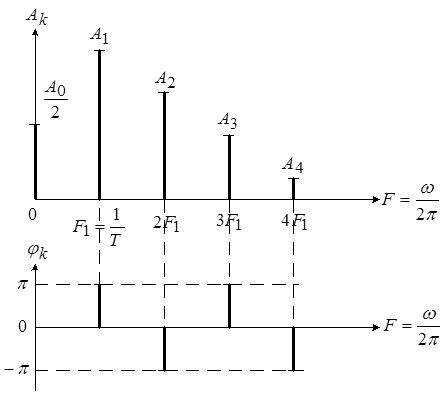
Рис. 1. Графическое изображение спектров амплитуд и фаз колебания
Каждая частотная составляющая изображается на графике спектра одним вертикальным отрезком – спектральной линией. Длина отрезка определяет величину амплитуды ![]() или начальной фазы
или начальной фазы ![]() , а местоположение отрезка на оси частот – частоту составляющей (
, а местоположение отрезка на оси частот – частоту составляющей (![]() ).
).
Иногда пользуются и табличным способом задания спектра (табл. 1).
Таблица 1
| Частота | 0 | ||||
| Амплитуда | |||||
| Начальная фаза | – |
--> ЧИТАТЬ ПОЛНОСТЬЮ <--