Реферат: Сплайны, финитные функции

1.5 Преобразование квадратичных кривых Безье в кубические

Квадратичная кривая Безье с координатами преобразовывается в кубическую кривую Безье с координатами:

2. Финитные функции

Финитной называется функция , определенная для всех , но отличная от нуля лишь на некоторой конечной области , называемой конечным носителем:

(2.1)

Для , определенных на , построение базиса из финитных функций осуществляется следующим образом. Сначала область , в которой решается задача, некоторым регулярным образом покрывается конечным числом перекрывающихся подобластей , например как на рис. 6.1:

(2.2)

Желательно, чтобы только для , смежных с .

Подобласти получили название конечные элементы.

Затем на каждом как на конечном носителе строим базисную финитную функцию . Все функции таким образом выбранного базиса линейно независимы в силу условий (2.1), (2.2).

Отметим преимущества такого выбора базиса:

а) ввиду того, что выбираются значительно меньшими и при этом скалярные произведения

(2.3)

равны нулю для функций с непересекающимися носителями, матрица проекционного уравнения будет сильно разрежена. Более того, если условие выполняется только для смежных носителей, то матрица получается ленточной, т.е. аналогична той, к которой приводят сеточные методы;

б) возможность выбора специфических приграничных конечных элементов и связанных с ними финитных функций, учитывающих особенности границы, позволяет эффективно решать краевые задачи на достаточно произвольной области .

Основная трудность аппроксимации финитными функциями состоит в сопряжении финитных функций на границах W_k таким образом, чтобы функция в целом была непрерывна вместе со своими производными достаточно высокого порядка.

При таком выборе базиса естественно поставить вопросы о его полноте, выборе вида функций и аппроксимационных свойствах разложения искомого решения

. (2.4)

На все эти вопросы частично дает ответ теория Стренга-Фикса.

2.2 Теория аппроксимации финитными функциями Стренга-Фикса

Изложим основные идеи этой теории для функций одной переменной с регулярными конечными элементами.

Область покрываем равномерной сеткой

, [p] – целая часть p.

Конечные элементы выберем как отрезки длиной с центром в точке : . Если , смежные элементы не пересекаются и их длина равна : если , то длина пересечения равна , длина равна ; при – длина пересечения , длина равна . Заметим, что такое покрытие полностью удовлетворяет условиям (2.2). Все базисные финитные функции с носителями выберем одинаковой формы как сдвиги одной «стандартной» финитной функции :

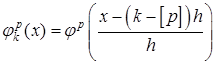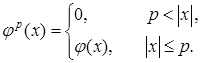; (2.5)

Если «стандартная» функция нормирована к единице, то ее сдвиги записываются в виде

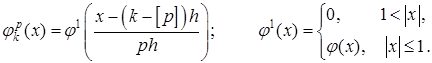(2.6)

Теорема Стренга-Фикса (один из вариантов)

Допустим, что . В этом случае для существует преобразование Фурье: