Реферат: Сплайны, финитные функции
Допустим, что для преобразования Фурье стандартной финитной функции ![]() выполнено условие
выполнено условие
![]() и
и 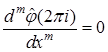 при
при ![]() (2.7)
(2.7)
(т.е. в ![]() точках
точках ![]() имеет нули
имеет нули ![]() й кратности).
й кратности).
Тогда существуют такие ![]() , что при
, что при ![]()
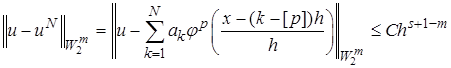 .
.
Это значит, что если, например, подобрать ![]() , у которой условия теоремы выполняются для
, у которой условия теоремы выполняются для ![]() , то аппроксимация самой функции
, то аппроксимация самой функции ![]() имеет порядок
имеет порядок ![]() , аппроксимация ее первой производной
, аппроксимация ее первой производной![]() , второй –
, второй – ![]() .
.
Наличие такой центральной теоремы, а также еще ряда доказанных Стренгом-Фиксом теорем, в частности о существовании функций, удовлетворяющих условиям (2.7), дает алгоритм для построения базисных финитных функций, обладающих необходимыми аппроксимационными свойствами.
3. B-сплайны Шёнберга
В вычислительной математике B-сплайном называют сплайн-функцию, имеющую наименьший носитель для заданной степени, порядка гладкости и разбиения области определения. Фундаментальная теорема устанавливает, что любая сплайн-функция для заданной степени, гладкости и области определения может быть представлена как линейная комбинация B-сплайнов той же степени и гладкости на той же области определения. [1] Термин B-сплайн был введён И. Шёнбергом и является сокращением от словосочетания «базисный сплайн». [2] B-сплайны могут быть вычислены с помощью алгоритма де Бора, обладающего устойчивостью.
В системах автоматизированного проектирования и компьютерной графике термин B-сплайн часто описывает сплайн-кривую, которая задана сплайн-функциями, выраженными линейными комбинациями B-сплайнов.
Когда узлы равноудалены друг от друга, говорят, что B-сплайн является однородным, в противном случае его называют неоднородным.
Когда количество узлов совпадает со степенью сплайна, B-сплайн вырождается в кривую Безье. Форма базисной функции определяется расположением узлов. Масштабирование или параллельный перенос базисного вектора не влияет на базисную функцию.
Сплайн содержится в выпуклой оболочке его опорных точек.
Базисный сплайн степени n: ![]() .
.
не обращается в нуль только на промежутке [ti, ti+n+1], то есть:
![]() . (3.1)
. (3.1)
Другими словами, изменение одной опорной точки влияет только на локальное поведение кривой, а не на глобальное, как в случае кривых Безье.
Базисная функция может быть получена из полинома Бернштейна
В-сплайн и некоторые наиболее часто используемые базисы
Теорема Стренга-Фикса указывает на то, что если стандартную финитную функцию ![]() выбрать исходя из условия (2.7), то ряд (2.4), построенный на основе ее сдвигов, будет обладать хорошими аппроксимационными свойствами.
выбрать исходя из условия (2.7), то ряд (2.4), построенный на основе ее сдвигов, будет обладать хорошими аппроксимационными свойствами.
Шенберг предложил один интересный класс функций, удовлетворяющих условию (2.7). Функцию ![]() называют В-сплайном (Шенберга) степени
называют В-сплайном (Шенберга) степени ![]() , если ее преобразование Фурье имеет вид
, если ее преобразование Фурье имеет вид
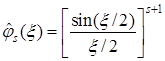 . (3.2)
. (3.2)
Как видим, функция (6.8) удовлетворяет всем условиям (6.7).
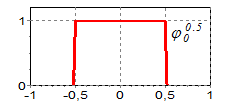
Базис из ступенек
Довольно просто показать, что при ![]()
|
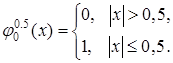 (3.3)
(3.3)
В этом случае базис представляет собой набор сдвигов (2.5) стандартной ступеньки ![]() (3.3), а функция
(3.3), а функция ![]() представляет собой разрывную ступенчатую функцию (
представляет собой разрывную ступенчатую функцию (![]() ). Аппроксимация по норме
). Аппроксимация по норме ![]() имеет порядок
имеет порядок ![]() . Такой базис может быть выбран в качестве второго базиса
. Такой базис может быть выбран в качестве второго базиса ![]() при использовании метода Галеркина-Петрова.
при использовании метода Галеркина-Петрова.
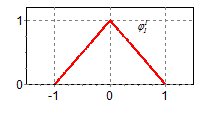
Базис из крышек
Рассмотрим В-сплайн степени ![]() :
: 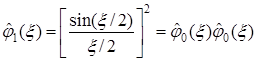 . Из этого соотношения следует, что
. Из этого соотношения следует, что ![]() получается как свертка функций
получается как свертка функций ![]() =
= 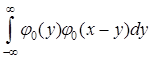
После несложных преобразований получаем:
|