Реферат: Статистическая механика классических систем

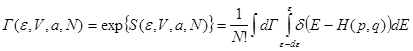(8.16)

Физической интерпретацией выражения (8.16) является определенный с точностью до постоянного компонента объем слоя 6N -мерного фазового пространства (p , q ) , заключенного между энергетическими гиперповерхностями и .

Несмотря на эквивалентность всех формализмов равновесной статистической механики, наибольшее распространение в классической теории получило каноническое распределение Гиббса и статистический интеграл . Это связано с удобством применения указанного распределения.

2. Как отмечалось раньше, гамильтониан классической нерелятивистской системы равен:

, (8.17)

причем, зависимость T (p ) не зависит от вида потенциала взаимодействий U (q ). Тогда распределение по импульсам также не зависит от вида потенциалов.

Подставляя (8.17) в (8.10), получаем:

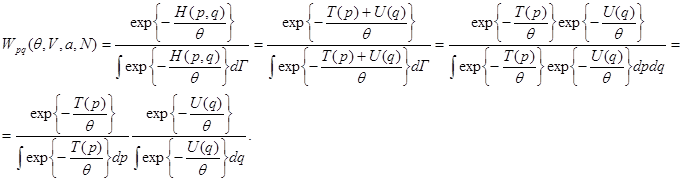
Выполняя в последнем равенстве интегрирование по координатам всех частиц, получаем распределение по импульсам:

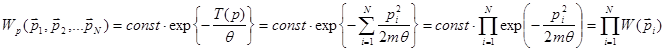(8.18)

Таким образом, из (8.18) следует мультипликативность распределения по импульсам в классической равновесной системе. Величина учтена при записи константы.

Мультипликативность распределения по импульсам приводит к тому, что оно распадается на произведение одинаковых распределений по импульсам каждой частицы:

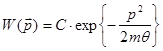(8.19)

Учитывая связь квадрата импульса частицы с компонентами вдоль каждой из координат: , получаем:

(8.20)

Тогда

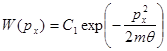, , (8.21)

Коэффициенты С₁ , С₂ и С₃ в (8.21) определяется из условий нормировки

(8.22)

Выполняя интегрирование в (8.22) и учитывая свойства интеграла Пуассона, получаем:

.

Подставляя полученный результат в (8.21) и учитывая (8.20) получаем распределение по импульсам частицы:

(8.23)

Выражение (8.23) может быть записано относительно скорости движения частиц (распределение по скоростям):

(8.24)

Выражение (8.24) представляет распределение Максвелла по скоростям частиц.

С математической точки зрения распределение (8.23) и, соответственно (8.21), представляет распределение Гаусса около среднего значения с дисперсией

(8.25)

Выражение (8.25) было получено без привлечения каких-либо дополнительных соображений, поэтому позволяет установить связь между температурой со средней кинематической энергией частиц. Из (8.25) непосредственно следует: