Реферат: Статистические методы в управлении качеством

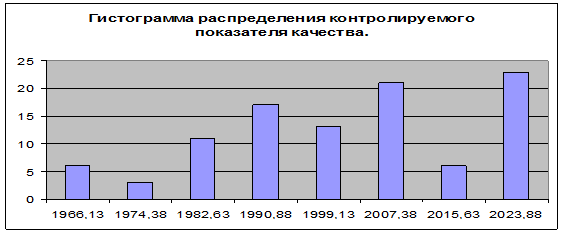
Рисунок 1 . Гистограмма распределения контролируемого показателя качества

3. Осуществить расчет параметров распределения и анализ полученных результатов.

Гистограмма позволяет оценить состояние исследуемого технологического процесса. Важную информацию может дать форма гистограммы и ее расположение в сравнении с контрольными нормативами (границами).

Возможны различные формы гистограмм:

1. с двусторонней симметрией (нормальное распределение);

2. вытянутая вправо (влево);

3. двугорбая;

4. в форме обрыва (обрезан один край или оба);

5. не имеющая высокой центральной части (плато);

6. с отдельным островком.

На рисунке 1 изображена гистограмма не имеющая высокой центральной части (плато) – такая гистограмма получается, когда объединяются несколько распределений, в которых средние значения отличаются незначительно. Такую гистограмму целесообразно анализировать, используя метод расслоения.

Гистограмма и границы поля допуска. Когда известны контрольные нормативы, на гистограмме отмечают прямыми линиями верхнюю и нижнюю границы нормы (допуска), что позволяет сравнить взаимное расположение гистограммы и контрольных нормативов. Если норма неизвестна, на график наносят точки, отображающие запланированные значения, и проводят через них вертикальные линии.

Разброс невелик по сравнению с нормой, но из-за большого смещения среднего значения xв сторону верхней границы нормы появляется брак. Необходимы меры, способствующие смещению среднего значения к средней точке между контрольными нормативами.

4. Выполните проверку гипотезы о нормальности эмпирического распределения контролируемого показателя качества – массы отливки с помощью χ_α ² – критерия Пирсона.

На рисунке 1 построена гистограмма эмпирического распределения значений контролируемого параметра.

Определим эмпирическую (статистическую) вероятность попадания случайной измеряемой величины в i-й интервал (частость): w_i = m_i / n, где m_i – число значений, попадавших в i-й интервал; n– общее число экспериментальных данных: , где k – число интервалов.

Номер интервала	Границы интервалов, г.		Центральное значение интервала x0 i , г.	Значение частоты mi	Значение частости wi
	нижняя	верхняя
1	1962	1970,25	1966,125	9	0,09
2	1970,25	1978,5	1974,375	5	0,05
3	1978,5	1986,75	1982,625	15	0,15
4	1986,75	1995	1990,875	14	0,14
5	1995	2003,25	1999,125	14	0,14
6	2003,25	2011,5	2007,375	18	0,18
7	2011,5	2019,75	2015,625	9	0,09
8	2019,75	2028	2023,875	16	0,16
Σ mi = 100	Σ wi = 1

Таблица 3 . Сгруппированные значения вариационного ряда контролируемого параметра качества

Расчет основных статистических характеристик.

1. Рассчитать среднее арифметическое значение результатов измерений:

2. Рассчитать среднее квадратичное отклонение (СКО):

.

.

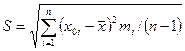3. Определить теоретическую вероятность попадания значений измеряемой величины в i–й интервал:

,

где - плотность нормированного нормального распределения;