Реферат: Статистическое исследование взаимосвязи социально-экономических показателей

Квадрат коэффициента корреляции называют коэффициентом детерминации (r² ). Коэффициент детерминации можно интерпретировать как долю общей дисперсии результативного признака (y), которая объясняется вариацией факторного признака (x).

Таблица 2

Оценка характера связи по линейному коэффициенту корреляции

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента: проверяется нулевая гипотеза об отсутствии связи между факторным и результативным признаками (H₀ : r = 0). Для проверки H₀ по формуле (1.1.11) следует рассчитать t-статистику (t_р ) и сравнить ее с табличным значением (t_т ), определяемым с использованием таблицы приложения 2 по заданным уровню значимости (α) и числу степеней свободы (d.f.). Если t_р > t_т , то гипотеза H₀ отвергается с вероятностью ошибки меньше чем α·100%. Это свидетельствует о значимости линейного коэффициента корреляции и статистической существенности зависимости между факторным и результативным признаками.

(1.1.11)

где k = n-2 для малой выборки,

k = n при большом числе наблюдений (n>100).

Аналогично оценивается значимость коэффициента регрессии; tр рассчитывают как отношение взятого по модулю коэффициента регрессии к его средней ошибке с заданными уровнем значимости (α) и числом степеней свободы d.f.= n-2.

(1.1.12)

1.5. Множественная корреляция и регрессия

При анализе взаимосвязей социально-экономических явлений, как правило, выясняется, что на результат влияет ряд факторных признаков, основные из которых следует включить в регрессионную модель. При этом следует помнить, что все факторы учесть в модели невозможно по ряду причин: часть факторов просто неизвестна современной науке, по части известных факторов нет достоверной информации или количество включаемых в модель факторов может быть ограничено объемом выборки (количество факторных признаков должно быть на порядок меньше численности изучаемой совокупности).

Множественная регрессия описывает форму связи в виде уравнения множественной регрессии, или регрессионной модели (табл.3).

Таблица 3

Основные виды множественной регрессии

– теоретическое значение результативного признака (y) при определенных значениях факторных признаков (x₁ , x₂ ,…, x_m ), подставленных в регрессионное уравнение;

а₀ – свободный член уравнения;

a₁ ,a₂ ,…,a_m – коэффициенты множественной регрессии.

Параметры уравнения множественной регрессии a₁ ,a₂ ,…,a_m называют коэффициентами множественной регрессии и определяют с помощью МНК путем решения системы нормальных уравнений МНК. При этом число нормальных уравнений в общем случае будет равно числу параметров. Если связь отдельного фактора с результатом не является линейной, то производят линеаризацию уравнения. Для упрощения решения системы нормальных уравнений значения всех признаков заменяют на отклонения индивидуальных значений признаков от их средних величин. Полученные коэффициенты множественной регрессии являются именованными числами и показывают, на сколько изменится результативный признак (по отношению к своей средней величине) при отклонении факторного признака от своей средней на единицу и при постоянстве (фиксированном уровне) других факторов.

Значимость коэффициентов множественной регрессии оценивается на основе t-критерия Стьюдента; t_р рассчитывают как отношение взятого по модулю коэффициента регрессии к его средней ошибке с заданными уровнем значимости (α) и числом степеней свободы d.f.= n-m-1.

Коэффициенты регрессии можно преобразовать в сравнимые относительные показатели - стандартизованные коэффициенты регрессии, или β-коэффициенты (1.1.13). β-коэффициент позволяет оценить меру влияния вариации факторного признака на вариацию результата при фиксированном уровне других факторов:

(1.1.13)

где σx_i – среднее квадратическое отклонение факторного признака,

σy – среднее квадратическое отклонение результативного признака,

a_i – коэффициент регрессии при соответствующем факторном признаке x_i .

При интерпретации результатов корреляционно-регрессионного анализа часто используют частные коэффициенты эластичности (Ex_i ). Коэффициент эластичности (1.1.14) показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного на 1% и при постоянстве (фиксированном уровне) других факторов:

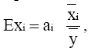(1.1.14)

где – среднее значение факторного признака,

– среднее значение результативного признака.

Множественная корреляция характеризует тесноту и направленность связи между результативным и несколькими факторными признаками. Основой измерения связей является матрица парных коэффициентов корреляции. По ней можно в первом приближении судить о тесноте связи факторных признаков между собой и с результативным признаком, а также осуществлять предварительный отбор факторов для включения их в уравнение регрессии. При этом не следует включать в модель факторы, слабо коррелирующие с результативным признаком и тесно связанные между собой. Не допускается включать в модель функционально связанные между собой факторные признаки, так как это приводит к неопределенности решения.

Более точную характеристику тесноты зависимости дают частные коэффициенты корреляции. Их удобно анализировать, если они представлены в табличном виде. Частный коэффициент корреляции служит показателем линейной связи между двумя признаками, исключая влияние всех остальных представленных в модели факторов. Например, для двухфакторной модели частный коэффициент корреляции между y и x₁ при фиксированном x₂ (r_yx1 /x₂ ) определяется в соответствии с (1.1.15).

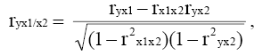(1.1.15)