Реферат: Статистическое исследование взаимосвязи социально-экономических показателей

Проверка значимости частных коэффициентов корреляции аналогична, как и для парных коэффициентов корреляции.

Множественный коэффициент корреляции (R) рассчитывается при наличии линейной связи между всеми признаками регрессионной модели. R изменяется в пределах от 0 до 1. Значимость множественного коэффициента корреляции проверяется на основе F-критерия Фишера. Например, в двухфакторной модели при оценке связи между результативным и факторными признаками для определения множественного коэффициента корреляции можно использовать формулу (1.1.16):

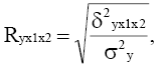или (1.1.16)

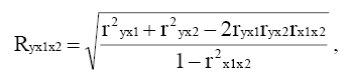
где δ² _{y x1x2} – дисперсия результативного признака, рассчитанная по регрессионному уравнению,

σ² _y – общая дисперсия результативного признака,

r_yx1 , r_yx2 , r_x1x2 – парные коэффициенты корреляции.

Квадрат множественного коэффициента корреляции называют множественным коэффициентом детерминации (R² ). R² оценивает долю вариации результативного фактора за счет представленных в модели факторов в общей вариации результата. Множественный коэффициент детерминации обычно корректируют на потерю степеней свободы вариации по формуле (1.1.17):

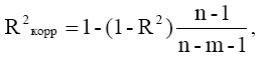(1.1.17)

где R² _корр – корректированный множественный коэффициент детерминации,

R² –множественный коэффициент детерминации,

n – объем совокупности,

m – количество факторных признаков.

Статистическая надежность регрессионного уравнения в целом оценивается на основе F-критерия Фишера: проверяется нулевая гипотеза о несоответствии представленных регрессионным уравнением связей реально существующим (H₀ : a₀ = a₁ =a₂ =…=a_m =0, R=0). Для проверки H₀ следует рассчитать значение F-критерия (Fр) и сравнить его с табличным значением (Fт), определяемым с использованием таблицы приложения 1 по заданным уровню значимости (α= 0,05) и числу степеней свободы (d.f.1=m-1 и d.f.2=n-m). Fр определяется из соотношения факторной и остаточной дисперсий, рассчитанных на одну степень свободы по формуле (1.1.18):

(1.1.18)

где D_факт , D_ост – суммы квадратов отклонений, характеризующие факторную и остаточную вариации результативного признака. В случае однофакторного дисперсионного комплекса D_факт и D_ост выражаются в соответствии с (1.1.19),

d.f.1 = m-1 – число степеней свободы факторной дисперсии,

d.f.2 = n-m – число степеней свободы остаточной дисперсии.

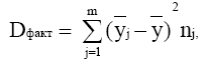(1.1.19)

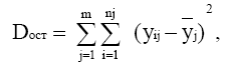
где y_ij , – значения результативного признака у i–й единицы в j–й группе,

i – номер единицы совокупности,

j – номер группы,

n_j – численность j–й группы,

– средняя величина результативного признака в j–й группе,

– общая средняя результативного признака.

Если Fр > Fт, то гипотеза H₀ отвергается. При этом с вероятностью 1-α= 0,95, или 95%, принимается альтернативная гипотеза о неслучайной природе оцениваемых характеристик, т.е. признается статистическая значимость регрессионного уравнения и его параметров.

1.6. Проверка адекватности регрессионной модели

Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным.

Корреляционный и регрессионный анализ обычно (особенно в условиях так называемого малого и среднего бизнеса) проводится для ограниченной по объёму совокупности. Поэтому показатели регрессии и корреляции – параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить, насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей.