Реферат: Связанные контура
Подставив значение ![]() из (7) в первое уравнение системы (6)
из (7) в первое уравнение системы (6)
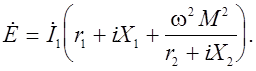
Освободившись от мнимости в знаменателе, получим
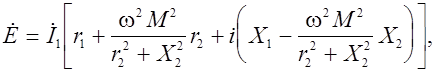
или
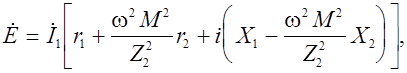
так как ![]() .
.
Поделив в полученном выражении приложенную э.д.с. на ток ![]() запишем выражение для эквивалентного входного сопротивления системы двух связанных колебательных контуров
запишем выражение для эквивалентного входного сопротивления системы двух связанных колебательных контуров
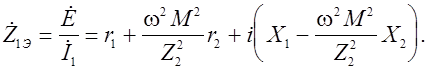 (8)
(8)
Модуль сопротивления Z 1Э равен
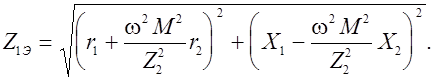 (9)
(9)
Анализ (8) показывает, что в результате связи первого контура со вторым в первый контур как бы вносятся два сопротивления: активное 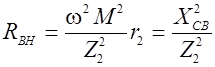
и реактивное  (10)
(10)
Таким образом, систему двух связанных колебательных контуров можно заменить одним эквивалентным контуром (рис. 2, б), в который вносится сопротивление
![]()
Суммарное активное сопротивление R 1э = r 1 + R вн всегда положительное, а знак суммарного реактивного сопротивления Х 1э =Х 1 +Х вн определяется настройкой каждого из контуров в отдельности (знаки X 1 и Х 2 и, следовательно, Х вн зависят от частоты, на которую настроен каждый контур).
Резонансные характеристики системы двух связанных контуров.
Под амплитудно-частотными резонансными характеристиками системы двух связанных контуров будем подразумевать зависимость амплитуд токов первого и второго контуров от частоты. Считая, что оба контура настроены на одну и ту же частоту w0 выделим модули тока первого и второго контуров при наличии связи между ними.
Если записать в символической форме ![]() и
и ![]() то
то
 (11)
(11)
где  Модуль (11) есть
Модуль (11) есть
![]() (12)
(12)
На основании (7), с учетом того что ![]() и
и ![]() имеем
имеем
 (13)
(13)
где ![]() и
и  . Запишем Модуль (13) с учетом (12) и (9)
. Запишем Модуль (13) с учетом (12) и (9)

Выражения (12) и (14) представляют собой уравнения резонансных характеристик для I 1 и I 2 соответственно в неявной относительно частоты форме. Таким образом, если построить зависимости модулей I 1 и I 2 от частоты, то это и будут амплитудно-частотные резонансные характеристики. При построении их будем исходить из двух случаев связи между контурами; слабой и сильной. Сначала займемся построением I 1 (w). Как видно из (12), частотную зависимость I 1 определяет частотная зависимость Z 1э (w), поскольку э. д. с. источника Е от частоты не зависит. Таким образом, построение сводится сначала к построению зависимости Z 1э (w), а затем — зависимости I 1 (w) как частного от деления Е на Z1э .
Выразив модуль Z 1э (w) через компоненты
![]()
построим попарно зависимости r 1 и r вн , Х 1 и Х вн от частоты, а Z 1э найдем графически, как геометрическую сумму r 1 + R вн и Х 1 + Х вн . I 1 строим в соответствии с (12). Построение проводим при небольших расстройках относительно резонансной частоты. Получаемые зависимости при слабой связи между контурами имеют вид, показанный на рис. 3, а при сильной связи—на рис. 4.
|
|
|
|
Рис. 3. Частотные зависимости входного сопротивления, его составляющих и тока I 1 системы двух связанных контуров при слабой связи между ними
Рис. 4 . Частотные зависимости входного сопротивления, его составляющих и тока I 1 системы двух связанных контуров при сильной связи между ними
Как видно, при слабой связи между контурами вследствие малости Х ВН по сравнению с Х 1 кривая X 1э (w) пересекает ось частот только в одной точке wо . При сильной связи между контурами вследствие значительной величины ХВН , которая на некоторых частотах превышает по абсолютной величине Х 1 , имея обратный знак, суммарная кривая Х1э (w) пересекает ось частот в трех точках: w01 , w0 и w02 . Другими словами, результирующее реактивное сопротивление системы равно нулю не только на частоте w0 , но и на частотах w01 и w02 , называемых частотами связи. Учитывая еще то обстоятельство, что при сильной связи между контурами сопротивления R ВН на частоте w0 и в близлежащей области большие, чем при слабой, понятен двугорбый характер кривых Z 1э (w) и I 1 (w) с максимумами на частотах w 1 и w 2 .
Очевидно, имеется граничная связь, превышение которой ведет к двугорбости амплитудно-частотной резонансной характеристики тока первичного контура. Такая связь называется первичной критической связью, а соответствующий ей коэффициент связи — первичным критическим коэффициентом связи (k кр1 ). Амплитудно-частотную резонансную характеристику вторичного тока строим на основании полученных характеристик первичного тока и (14). Для того чтобы можно было сравнивать амплитудно-частотные резонансные характеристики первичного и вторичного токов, их надо строить на одном рисунке по отношению к резонансным значениям Z 2 , т.е. ![]() и.
и. ![]() . Согласно (14)
. Согласно (14)  Таким образом , для построения амплитудно-частотных характеристик вторичного тока достаточно перемножить координаты кривых I 1 (w) / I 1p и r 2 /Z 2 (w)
Таким образом , для построения амплитудно-частотных характеристик вторичного тока достаточно перемножить координаты кривых I 1 (w) / I 1p и r 2 /Z 2 (w)
Указанные построения для связи, меньше критической, выполнены на рис. 5, а, а для связи, больше критической,— на рис. 2. 19, б. Как видно из рис. 5, б, двугорбость кривой первичного тока выражена резче, причем горбы разнесены дальше, чем у кривой вторичного тока. Очевидно, возможна такая связь между контурами системы, когда двугорбость первичного тока уже наступит, а вторичного — еще нет. Такая связь, превышение которой ведет к появлению двугорбости у резонансной амплитудно-частотной характеристики вторичного тока, называется вторичной критической связью, а соответствующий ей коэффициент связи -вторичным критическим коэффициентом связи (k кр2 ).
Рис. 5. Амплитудно-частотные характеристики вторичного тока системы двух связанных контуров при слабой (а) и сильной (б) связях между ними

