Реферат: Связанные контура

Подставив значение Х _св.опт в выражение для тока I _2mах , можно найти самый большой максимум тока во втором контуре

(28)

Однако на практике используют так называемый метод полного резонанса, при котором сначала достигается равенство Х _1э = 0 по опи­санному второму способу настройки, когда каждый контур системы настраивается в резонанс независимо от другого. Затем подбирается оптимальная связь между контурами по самому большому току во втором контуре (I_{2max max} ). В случае полного резонанса при измене­нии связи между контурами подстройка их для выполнения условия

Х _1э = Х ₁ -Х _cв ² /Z ₂ =0 нужна, так как ввиду того что Х ₁ = Х ₂ = 0, это условие выполняется при любой связи.

Обратимся в случае полного резонанса к выражению для тока во втором контуре (14) и исследуем его на экстремум, т. е. определим оптимальную связь, обеспечивающую I _{2max max} , как это было сделано при сложном резонансе. С учетом того, что Х ₁ = Х ₂ = 0, (14) принимает вид

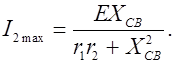
Взяв производную тока I _2max по Х _св

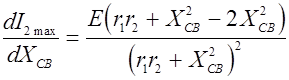
и приравняв ее к нулю, найдем

или

где

Таким образом, в случае полного резонанса также подтверждено, что при оптимальной связи r ₁ =R _вн , причем При подстановке этого значения в выражение для I _2max получаем Как видно из сравнения последнего выражения с (28), значение самого большого тока во втором контуре при сложном и полном резонансах одинаковое, но в случае сложного резонанса оно до­стигается при большем значении Х _св.опт , т.е. при большей связи между контурами.

Прохождение радиоимпульса через двухконтурную связанную систему

Для анализа возьмем импульс с прямоугольной огибающей. Частота заполнения не модулирована и равна w₀ . Амплитуда импульса равна 1в, а Q₀ =0.

В качестве двухконтурной избирательной системы рассматривается полосовой усилитель схематически изображенный на рис. 8. Контуры идентичны, резонансные частоты контуров w_р1 =w_р2 =w_р =w₀ . Таким бразом, в данном случае Dw = 0.

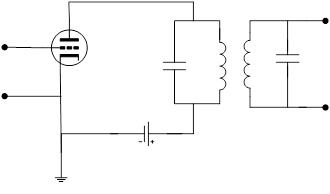
Рис. 8.

Передаточная функция такого усилителя

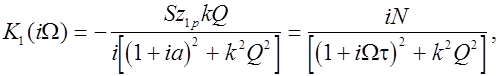(29)

где

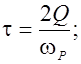
Заменяя i W на Р, получаем

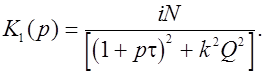(30)

Обратимся к опредилению сигнала на выходе системы. Сначала рассмотрим явления на фронте импульса. При этом задача сводится к включению гармонической э.д.с. в момент t = 0. Подставив в общее выражение спектральную плотность S_A (p) по формуле 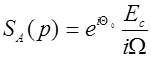и коэффициент передачи К _1(p) по формуле (30), получим

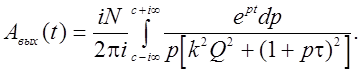
Полюсы подынтегральной функции

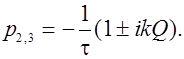
Определяя вычеты, получим следующее окончательное выражение для комплексной огибающей выходного сигнала (угол Q₀ принят равным нулю)

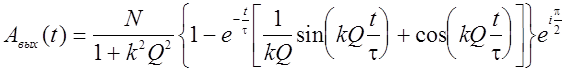(31)

Вчастном случае ‘критической связи’ (kQ = 1) получаем

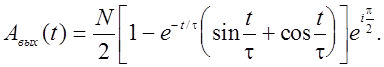(32)

Множитель e^{i p /2} учитывет сдвиг фазы выходного напряжения на 90⁰ относительно входного сигнала.

График 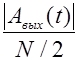изображен на рис. 9 (участок от t = 0 до t = T ).

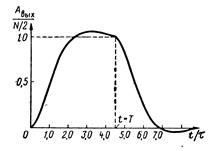
Рис. 9.

Рассмотрим теперь явления в цепи в конце импульса, начиная с момента t = T , где T – длительность импульса. Ясно, что после прекращения действия внешней силы в системе может существовать только свободное колебание. Структура этого колебания легко может быть выявлена, если прекращение импульса рассматривать как результат включения в момент t = T новой э.д.с., компенсирующей э.д.с. сигнала. Для этой компенсируещей э.д.с. решение имеет такой же вид, как и (31), но отличается только знаком, который должен быть обратным знаку правой части выражения (31), и сдвигом начала отсчета времени из нуля в точку t = T .

Так как к моменту t = T затухающую часть выражения (31) можно считать равной нулю, то комплексная огибающая результирующего сигнала на выходе для t > T должна иметь вид

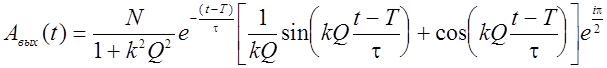
Построенный по этой формуле график 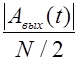для kQ =1 изображен на рис. 9 (участок t > T ).

литература

1. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Советское радио, 1971.

2. Комлик В.В. Радиотехника и измерения. Изд-во ‘Вища школа’, Киев, 1978.