Реферат: Техника и электроника СВЧ (Часть 1)

Маємо ділянку, де , тобто маємо уповільнення. Це – звичайний резонатор для ЕМ – хвилі. При розрахунках у нас переходило в , а це можливо при . Це – ще одна умова.

Спіраль.

Тут , . Така система по своїй конструкції уповільнююча, з коефіцієнтом уповільнення . Але тут теж є резонансні ефекти, що призводять до уповільнення, якщо .

Лекція 14

Об’ємні резонатори.

У них хвиля “б’ється” між стінками (див. Мал.):

, тоді хвиля, що заходить у резонатор, і відбита, будуть у фазі; тобто це – умова резонансу.

Розв’яжемо рівняння Максвела для даної системи – знайдемо коливання, що існують у цій коробці.

. З урахуванням граничних умов на бокових стінках (стінках хвильовода): . Накладемо ще дві граничні умови: звідки одержимо - неправильно. Це тому, що не врахували відбиття від торців; правильно буде записати:

. Тоді при накладанні умови одержимо .

.

Розглянемо , одержимо . Тоді .

Типи коливань: (останній індекс – кількість півхвиль)

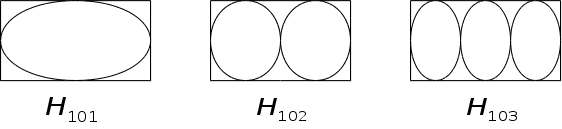
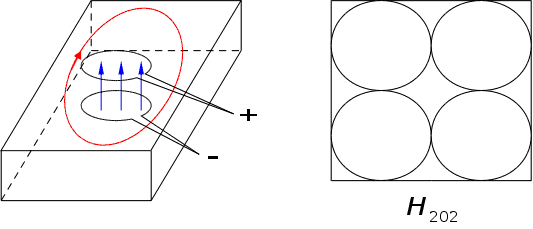
В круглому резонаторі:

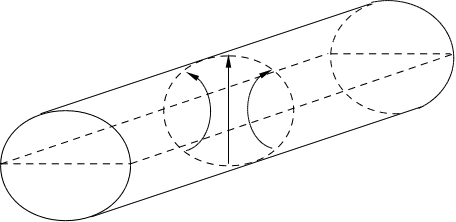
Існує дуже багато типів резонаторів. Наприклад, резонатор хвилі, що біжить, такий резонатор ще називають кільцевим. Резонанс: .

Добротність резонаторів .

Для будь-якого резонатора звичайно існує АЧХ, яка має ширину.

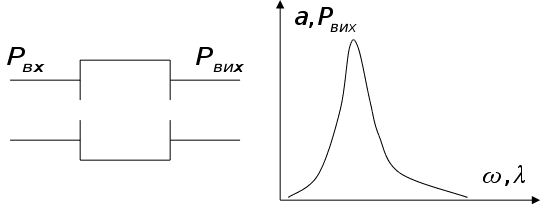
Напівширина вимірюється для на 0.5; а для вихідної амплітуди – на 0.7 висоти контуру. . Хвиля затухає із декрементом : , . Доведемо, що . Це випливає з розв’язку рівняння: . Втрати - тут добротність . Втрати можуть бути в металі, на випромінювання в діелектрику:

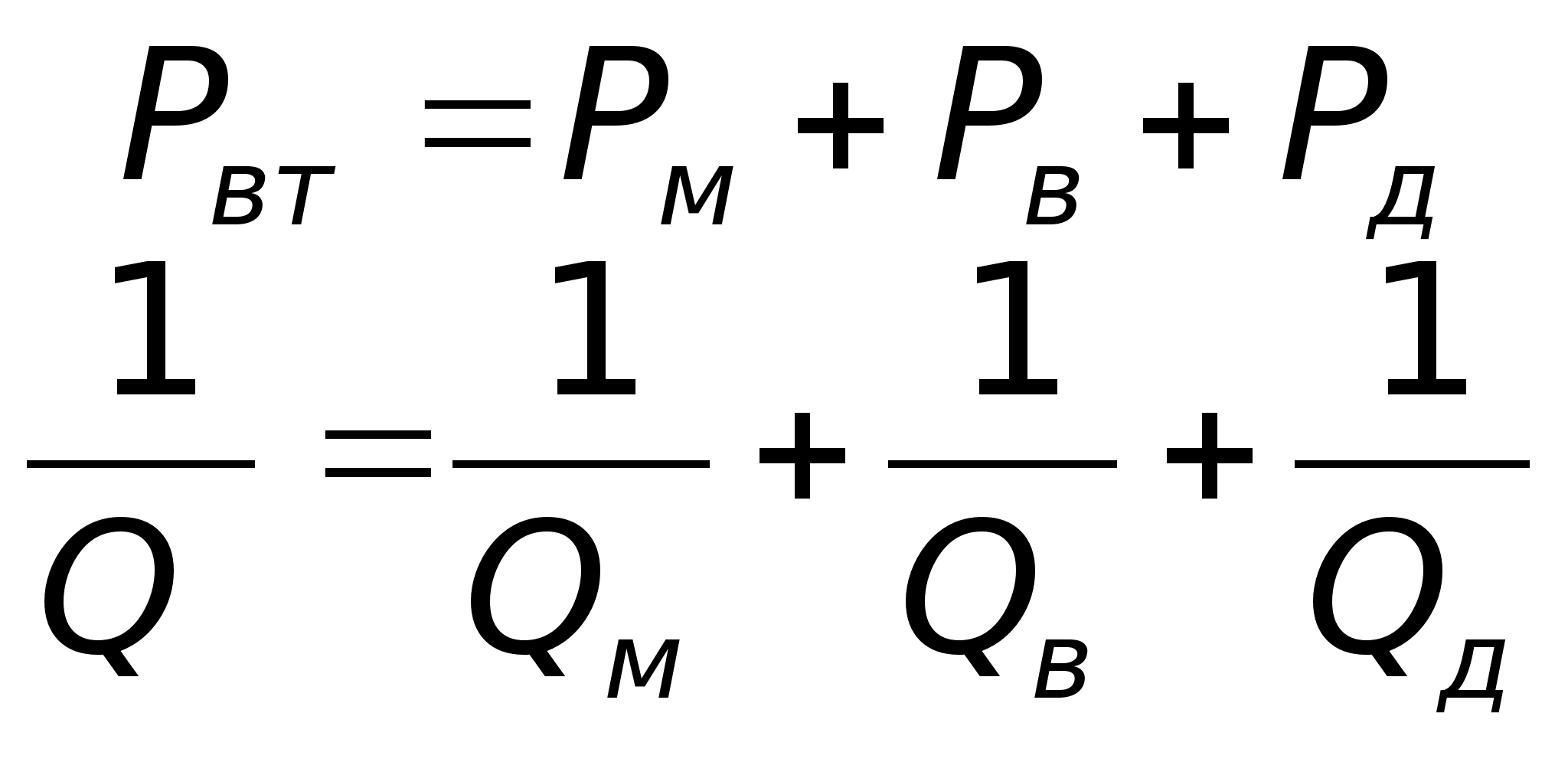
Підрахуємо добротність, пов’язану з втратами у діелектрику:

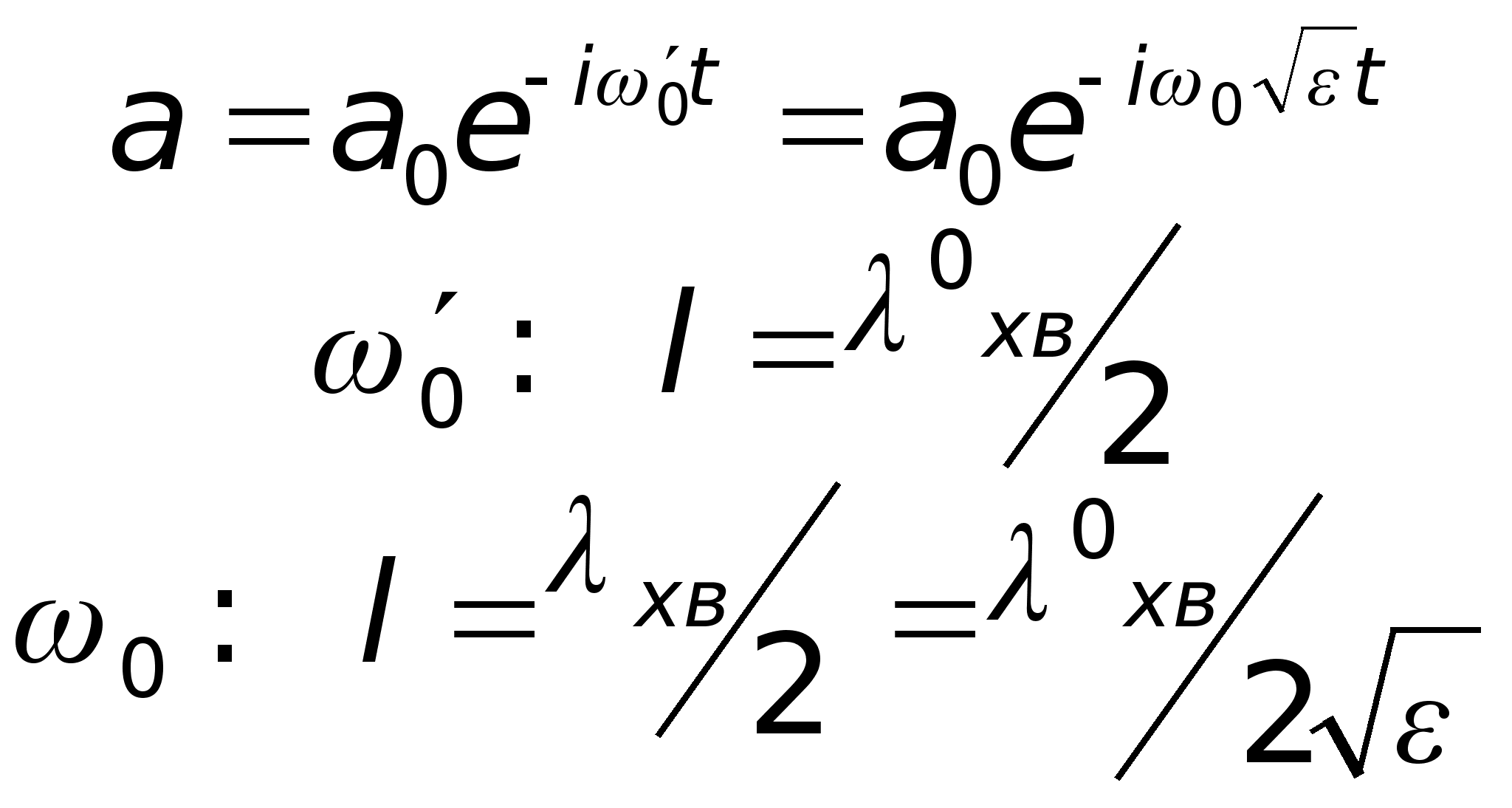
Таким чином, ( - коливання резонатора з діелектриком, - порожнього) .

, де 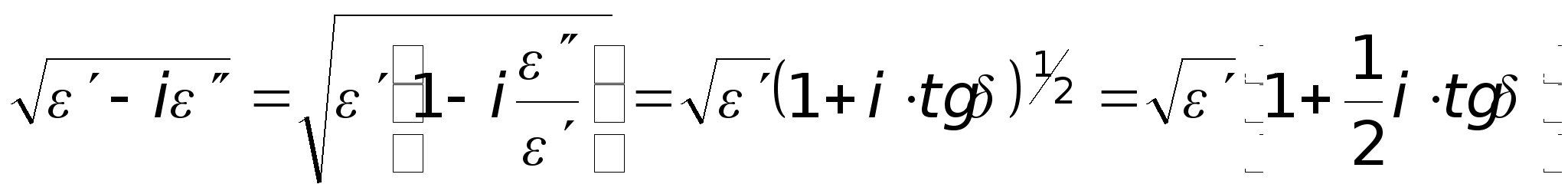, отже . Таким чином ми одержали , . Для розрахунку в металі треба знайти потік енергії (як у смушковому резонаторі).

Лекція 15

Відкриті резонатори.

Це резонатори на основі відкритих ліній передач. Вони мають електромагнітний контакт з відкритим простором. Звичайно використовуються в лазерах сферичні діелектричні резонатори. Нас цікавлять шари діелектрика для лінії . Тут не можна використовувати геометричні наближення, потрібно розв’язувати рівняння Максвела.