Реферат: Температурный расчет с помощью вычислений информационной математики

q(IIX,P)=100

enddo

N=NN

end

ТЕСТ

Для тестирования составлю разностную систему с шагом вдоли оси X и Y=0.05

Неизвестные значения в узлах матрицы находящихся внутри фигуры высчитываются по формуле:

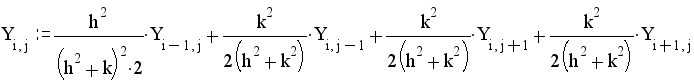
Неизвестные значения в узлах матрицы находящихся на оси симметрии высчитываются по формуле:

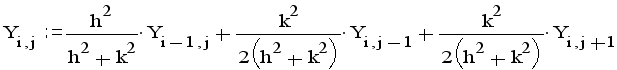
МЕТОД ЗЕЙДЕЛЯ.

Метод Зейделя относится к числу итерационных методов, в которых принципиально отсутствует фактор накопления погрешностей. Поэтому он широко применяется для решения больших систем уравне­ний. Будем рассматривать корни решаемой системы как компоненты некоторого вектора у . Основная идея всех итерационных методов заключается в том, что берется приближенное значение вектора у и по формулам, составленным на основании решаемых уравнений, вычис­ляется новое приближенное значение вектора у . Назовем эти при­ближенные значения y(k) и y(k+1) соответственно. Поскольку ис­ходное приближение выбиралось произвольно, то у(k+1)в свою очередь может послужить исходным для получения по тем же формулам нового приближения y(k+2) . Очевидно, этот процесс можно продолжать сколь угодно долго. Говорят, что процесс итераций сходится, если получаемая при этом последовательность векторов у(k) (к=0,1,2,...} имеет своим пределом вектор y,являющийся точным решением системы:

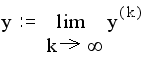
На практике невозможно достигнуть этого предела, но можно прибли­зиться н нему с любой наперед заданной точностью. Так и поступают задаются некоторой погрешностью, вектором начального приближе­ния и получают последовательные приближения до тех пор, пока дей­ствительная погрешность корней не станет меньше заданной.

Различные методы отличаются друг от друга способом вычисления очередного приближения, но во всех методах существуют две главные проблемы:

обеспечение сходимости процесса итераций;

оценка достигнутой погрешности.

Пусть дана линейная система

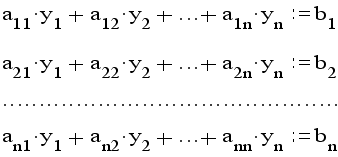
Предполагая, что диагональные коэффициенты

aii<>0 (i=1,2,..,n)

разрешим первое уравнение относительно y1 , второе - относите­льно y2 и т.д.

Тогда получим эквивалентную систему

где

при i<>j

и

при i=j (i,j=1,2,...,n)