Реферат: Температурный расчет с помощью вычислений информационной математики

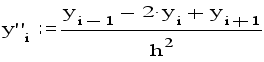
При определении разностей в i -и точке использовались значения функции в точках, расположенных симметрично относительно xi . Поэтому эти разности назы­ваются центральными.

Существуют также левые и правые разности, использующие точки, расположенные соответственно левее и правее точки xi. С помощью этих разностей можно также приближенно вычислять значения производных, но погрешность при этом будет больше -порядка h.

Разностные системы уравнений составляются в следующем порядке.

1. Исходное дифференциальное уравнение преобразуют к та­кой форме, чтобы затем получить из него наиболее простую разностную систему уравнений. При этом учитывают, что коэффициен­ты при производных войдут в разностную схему одновременно в несколько ее членов и затем будут распространены на всю систе­му уравнений. Поэтому желательно иметь единичные коэффициенты при производных в исходном уравнении.

2. На интервале интегрирования исходного уравнения уста­навливают равномерную сетку с шагом h и записывают разностную схему, приближенно заменяя производные соответствующими цент­ральными конечно-разностными отношениями.

3.Применяя разностную схему для узлов сетки записывают разностные уравнения. При этом можно получить уравнения содержащие так называемые внеконтурные неизвестные, то есть неизвестные в точках, лежащих за пределами установленной сет­ки.

4.В разностной форме записывают краевые условия и состав­ляют полную систему разностных уравнений.

Оценка погрешности решения краевой задачи

Решение разностной системы уравнений дает приближенное решение краевой задачи. Поэтому возникает вопрос о точности этого приближенного решения.

Для линейных краевых задач доказана теорема о том, что по­рядок точности решения краевой задачи не ниже порядка точности аппроксимации производных конечно-разностными отношениями. Оценку погрешности производят при­емом Рунге. Краевую задачу решают дважды: с шагом сетки h и с шагом сетки H=kh, погрешность решения с малым шагом h оценивают по формуле:

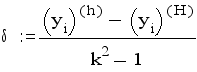
где y(h) и y(H) - решения, полученные для одной и той же точ­ки -xi отрезка интегрирования с разными шагами. Относительную погрешность E оценивают по формуле:

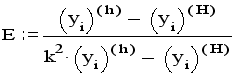
Если при составлении разностной системы уравнений исполь­зуются левые или правые разности, то погрешность решения будет выше, порядка 0(h), и для ее оценки в формулах следует заменить k*k на k .

Применение метода конечных разностей для решения уравнений в частных проиэводных

Для применения разностного метода в области изменения не­зависимых переменных вводят некоторую сетку. Все производные, входящие в уравнение и краевые условия, заменяют разностями значений функции в узлах сетки и получают таким образом алгебраическуго систему уравнений. Решая эту систему, находят приб­лиженное решение задачи в узлах сетки.

Блок схема.

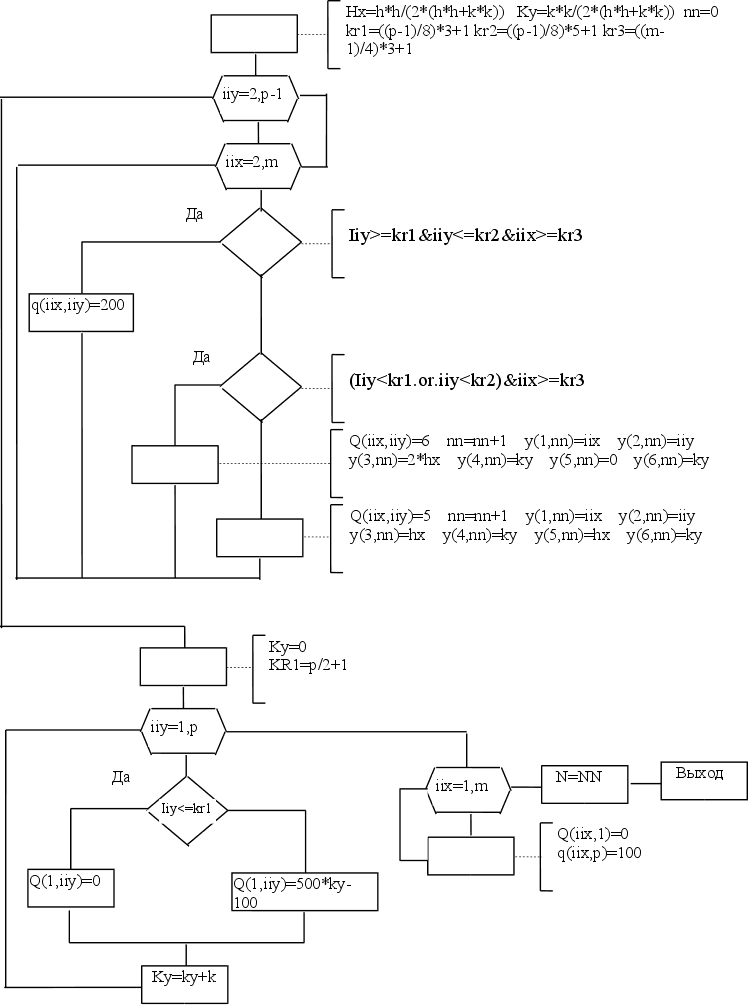
Подпрограмма МКР.

c------------------------------------------------------------------

c ПОДПРОГРАММА СОСТАВЛЕНИЯ СИСТЕМЫ УРАВНЕНИЙ

c МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ

c

c real H-шаг по оси X

c real K-шаг по оси Y

c real N-количество уравнений(примерное число,желательно N=M*P)

c real y(6,N)-выходной массив уравнений,содержащий следующие поля:

c y(1,N)-номер точки по оси X