Реферат: Теоретические основы математических и инструментальных методов экономики
В – матрица-столбец свободных членов
Векторная форма записи общей задачи линейного программирования
F = CX → max (min)
при ограничениях
![]()
Х≥0,
где СХ – скалярное произведение векторов
С = (С1 , С2 , …, Сn ) и Х = (х1 , х2 , …, хn ),
векторы
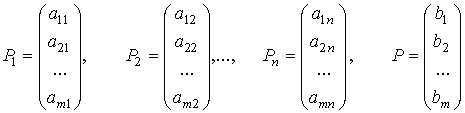
состоят соответственно из коэффициентов при переменных и свободных членов.
(про функционал)
В общем случае задача оптимизации формулируется как задача отыскания maxили minзначения I(v) для ![]() .
.
Под решением такой задачи понимается такое ![]() , что для остальных элементов
, что для остальных элементов ![]() выполняется неравенство
выполняется неравенство ![]() или
или ![]() в зависимости от требований задачи.
в зависимости от требований задачи.
При этом:
v – некоторая функция
I(v) – функционал вида 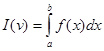
Многокритериальная оптимизация. Методы сведения многокритериальной задачи к однокритериальной. Метод уступок. Методы определения уровня предпочтений. Способы поиска паретовского множества альтернатив.
Многокритериальная оптимизация представляет собой минимизацию некого вектора целей F(x), на которой могут быть наложены дополнительные ограничения или предельные значения:
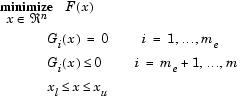 | (3-47) |
Отметим, что поскольку F(x) является неким вектором, то любые компоненты F(x) являюся конкурирующими и отсутсвует некое единое решение поставленной задачи. Взамен этого, для описания характеристик целей вводится концепция множества точек неулучшаемых решений [41] (так называемая оптимальность по Паретто [4],[6]). Неухудшаемое решение есть такое решение, в котором улучшение в одной из целей приводит к некому ослаблению другой. Для более точной формулировки данной концепции рассмотрим некую область допустимых решений ![]() в параметрическом пространстве
в параметрическом пространстве ![]() , которое удовлетворяет всем принятым ограничениям, т.е.
, которое удовлетворяет всем принятым ограничениям, т.е.
| (3-48) |
при ограничениях
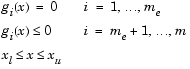
Отсюда возможно определить соответствующую область допустимых решений для пространства целевых функций ![]() .
.
| (3-49) |
Точка неулучшаемого решения может быть определена как:
Определение. Точка ![]() является неулучшаемым решением, если для некоторой окрестности
является неулучшаемым решением, если для некоторой окрестности ![]() нет некого
нет некого ![]() такого, что
такого, что ![]() и
и
| |
Стратегия взвешенных сумм
Данная стратегия взвешенных сумм преобразует многокритериальную задачу минимизации вектора ![]() в некую скалярную задачу путем построения неких взвешенных сумм для всех выбранных объектов.
в некую скалярную задачу путем построения неких взвешенных сумм для всех выбранных объектов.
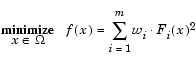 | (3-51) |
Далее уже к данной задаче оптимизации уже может быть применен стандартный алгоритм оптимизации без наличия ограничений. В этом случае рассматриваются взвешенные коэффициенты для каждой из выбранных целей. Взвешенные коэффициенты необязательно должны напрямую соответствовать относительной значимости соответствующей цели или принимать во внимание взаимовлияние между конкретно выбранными целями. Более того, границы неулучшаемых решений могут быть и не достигнуты, так что определенные решения являются по существу недостижимыми.
Метод ![]() -ограничений
-ограничений
Некий определенный способ, который отчасти позволяет преодолеть проблему выпуклости метода взвешенных сумм, есть метод ![]() -ограничений. В этом случае осуществляется минимизация основной цели
-ограничений. В этом случае осуществляется минимизация основной цели ![]() и при представлении остальных целей в форме ограничений типа неравенств.
и при представлении остальных целей в форме ограничений типа неравенств.
| (3-52) |