Реферат: Теоретические основы математических и инструментальных методов экономики
Методы субградиентной оптимизации . Эти итеративные процедуры формируют последовательность векторов {lk }. Начиная с некоторого начального значения l 0 эти вектора меняются по следующему правилу
lk+ 1 = lk + tk (A xk - b ),
где xk — оптимальное решение задачи ![]() , а tk — размер шага. Фундаментальный теоретический результат заключается в том, что [14]
, а tk — размер шага. Фундаментальный теоретический результат заключается в том, что [14]
![]() .
.
Размер шага на практике обычно выбирают, следуя [11],
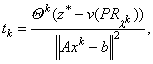
где q k — скаляр, 0 < q k ![]() 2 и z* — верхняя граница для n(D). Обычно z* получают эвристикой для P. В методе ветвей и границ z* — текущий рекорд. Последовательность q k , как правило, начинается с q 0 = 2 и затем q k делится пополам, через фиксированное число итераций, зависящее от размерности задачи.
2 и z* — верхняя граница для n(D). Обычно z* получают эвристикой для P. В методе ветвей и границ z* — текущий рекорд. Последовательность q k , как правило, начинается с q 0 = 2 и затем q k делится пополам, через фиксированное число итераций, зависящее от размерности задачи.
Элементы функционального анализа. Метрические, линейные и нормированные пространства. Эвклидово пространство. Гильбертово пространство. Линейные операторы и функционалы в линейных нормированных пространствах
Функциональный анализ, часть современной математики, главной задачей которой является изучение бесконечномерных пространств и их отображений. Наиболее изучены линейные пространства и линейные отображения. Для Ф. а. характерно сочетание методов классического анализа, топологии и алгебры. Абстрагируясь от конкретных ситуаций, удаётся выделить аксиомы и на их основе построить теории, включающие в себя классические задачи как частный случай и дающие возможность решать новые задачи. Сам процесс абстрагирования имеет самостоятельное значение, проясняя ситуацию, отбрасывая лишнее и открывая неожиданные связи. В результате удаётся глубже проникнуть в сущность математических понятий и проложить новые пути исследования.
Развитие Ф. а. происходило параллельно с развитием современной теоретической физики, при этом выяснилось, что язык Ф. а. наиболее адекватно отражает закономерности квантовой механики, квантовой теории поля и т.п. В свою очередь эти физические теории оказали существенное влияние на проблематику и методы Ф. а.
1. Линейные пространства. Базис
Одно из основных понятий современной математики - линейное пространство.
Пусть L - некоторое множество объектов произвольной природы, а C - множество комплексных чисел. Множество L называют линейным пространством, если на нем определены две операции: 1) операция сложения любых двух элементов этого множества и 2) операция умножения элементов этого множества на комплексное число, причем эти операции удовлетворяют некоторым естественным аксиомам. Более точно:
Определение . Множество L называется линейным пространством над полем комплексных чисел C, если
- каждой паре элементов x, y из этого пространства поставлен в соответствие элемент z этого пространства, называемый суммой элементов x и y (обозначение:
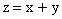 );
); - каждому элементу x из L и каждому комплексному числу поставлен в соответствие элемент из L, называемый произведением и x (и обозначаемый
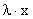 или x);
или x); - указанные операции удовлетворяют следующим аксиомам:
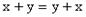 для любых
для любых 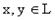 ,
, 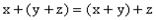 для любых
для любых 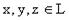 ,
, - существует "нулевой" элемент
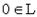 , такой, что
, такой, что 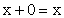 для любого
для любого 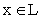 ,
, - для каждого
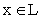 существует "противоположный" ему элемент
существует "противоположный" ему элемент 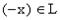 , такой, что
, такой, что 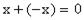 ,
, 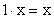 для любого
для любого 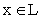 ,
, 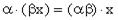 для любого
для любого 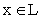 и любых
и любых 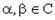 ,
, 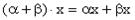 для любого
для любого 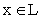 и любых
и любых 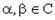 ,
, 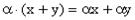 для любого
для любого 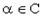 и любых
и любых 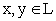 .
.
Подчеркнем, что перечисленные аксиомы являются естественным обобщением хорошо известных свойств сл?