Реферат: Теорія фірми

2) відношення граничних продуктивностей факторів дорівнює відношенню їхніх цін

, ;

3) гранична продуктивність факторів, що припадає на грошову одиницю, в оптимальному плані має бути однаковою для всіх факторів виробництва

, .

Дані співвідношення складають основу теорії граничної продуктивності (теорії вартості).

3. Модель рівноваги фірми

Припустимо метою фірми є максимізація прибутку шляхом вибору видів витрат при заданій виробничій функції , заданій ціні випуску продукції і цінах витрат (оплата факторів виробництва) .

Прибуток дорівнює річному валовому доходу за винятком витрат виробництва , тобто . Валовой річний доход обчислюється як річна продукція, помножена на її ціну

.

Витрати виробництва дорівнюють загальним виплатам за всі види витрат

.

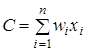Розв’язуючи довгострокову задачу, фірма вільна вибрати будь-який вектор витрат із простору витрат, тому задача формулюється в такий спосіб:

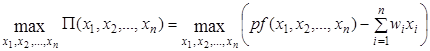(6)

за умови .

Задача (6) є задачею математичного програмування, єдиним обмеженням якої є невід’ємність компонентів вектора витрат.

Необхідні умови виражаються системою

, ,(7)

де – оптимальний план.

З (7) випливає, що , , де – вартість граничної продуктивності -го фактора, тобто вартість додаткового випуску, визначена як результат додаткових витрат -го виду в точці оптимального вибору цих витрат.

Під час розв’язання короткострокової задачі на фірму накладаються обмеження, наприклад, на вектор витрат, тобто фірма не може закупати деякі фактори виробництва вище певного рівня. Тоді задача (6) матиме такий вигляд:

(8)

за умови й , .

Якщо система обмежень в (8) – опукла множина, а – увігнута функція, то задача (8) є задачею опуклого програмування, що розв’язується методом штрафних функцій або його модифікаціями.

4. Алгоритм розв’язання задачі поведінки фірми. Метод Ероу-Гурвіца

Розглянемо задачу (8) визначення максимального значення ввігнутої функції за умови й , , де система обмежень є опуклою множиною.

Замість того, щоб безпосередньо вирішувати цю задачу, знайдемо максимальне значення функції

,

що є сумою цільової функції задачі (8) і деякої функції , обумовленою системою обмежень, яка називається штрафною функцією. Штрафну функцію побудуємо так:

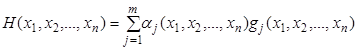, (9)