Реферат: Теорія фірми

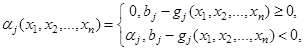
Або

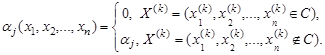(10)

В (10) – деякі постійні числа, які є ваговими коефіцієнтами. В класичному методі штрафних функцій значення вибирають довільно, причому, чим менше , тим швидше визначають прийнятний розв’язок, однак точність його знижується. Недолік довільного вибору усувається під час розв’язання задачі (8) методом Ероу-Гурвіца, відповідно до якого на черговому кроці числа обчислюються за формулою

, , (11)

де за беруть довільні невід’ємні числа, а – крок обчислень, який, як правило, дорівнює .

5. Недосконала конкуренція. Монополія та монопсонія

Модель рівноваги фірми (6) будується на класичному припущенні про досконалу конкуренцію, тобто для випадку фіксованого задання цін на продукцію й витрати.

Однак, у багатьох випадках фірма характеризується монополію, тобто має монопольну владу впливати на ціну продукції, або монопсонією, тобто володіє деякою монопольною владою впливати на ціни витрат (факторів виробництва).

Монополіст має можливість впливати на ціну продукції шляхом варіювання випуску своєї продукції , для якої криву попиту можна записати в такому вигляді: – функція попиту на випуск продукції. Дана функція характеризує ціну, яку фірма може призначити при різних рівнях пропозиції продукції. В загальному випадку фірма може знизити свою ціну для того, щоб продати більше продукції, тому .

Оскільки валовий річний доход визначається як , тоді . Граничний річний доход фірми визначається як зміна річного доходу в міру того, як змінюється випуск продукції

. (12)

На випадок монополії в формулі (12) граничний доход виявляється менший за ціну продукції

.

Монопсоніст може вплинути на ціну витрат шляхом варіювання своїх покупок даного виду факторів виробництва

,

Ця функція характеризує плату фірми за витрати при різних рівнях попиту на них.

Взагалі фірма може купувати більшу кулькість даного фактора вироб-ництва, тільки якщо запропонує більш високу ціну за нього, тобто , .

Через те, що вартість витрат -го виду можна подати у вигляді , , а граничну вартість витрат -го виду, що відображає зміну у вартості цих витрат при збільшенні їхньої кількості, можна навести у вигляді

, (13)

то на випадок монопсонії гранична вартість витрат перевищує їхню оплату.

Задачу фірми в умовах недосконалої конкуренції можна подати у такому вигляді:

(14)

за умови .

Введемо функцію Лагранжа для задачі (14)

.

Необхідні умови для знаходження оптимального розв’язку визначають прирівнюванням до нуля всіх часткових похідних функції Лагранжа

,

, ,