Реферат: Теория флюксий
Частное решение.
«Так как эта проблема обратна вышеизложенной, то ее можно решать с помощью противоположных действий, а именно, члены помноженные на 
, должны быть расположены по степеням x и поделены на 
, а затем - на показатели их степеней или же на какую-либо другую арифметическую прогрессию. После того как эти действия будут произведены и для членов, помноженных на 
, 
или 
, получившуюся при этом сумму по отбрасывании лишних членов следует положить равной нулю.
Пример 2.
Предложено уравнение
Действие производится следующим образом:
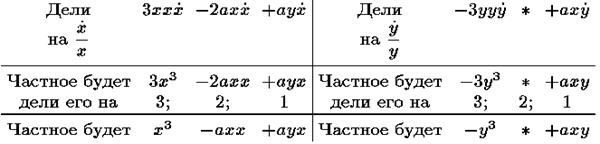
Поэтому сумма
|
выражает искомое соотношение величин x и y .
Здесь следует заметить, что хотя член axy встречается дважды, я все же не выписываю его дважды в сумме
|
но один из них отбрасываю как лишний. Таким образом, если какой-либо член встречается дважды (или еще больше раз в том случае, если он получается от различных флюэнт), то в сумме членов его следует выписывать лишь один раз.»
( Здесь описана следующая процедура нахождения частного решения дифференциального уравнения
|
Уравнение записывается в виде
|
откуда вытекает наличие решения
|
Произвольной постоянной Ньютон не добавляет).
Далее Ньютон пишет: «Прочие необходимые замечания я оставляю на долю проницательности самого мастера, тем более, что было бы излишним чересчур долго останавливаться на этом предмете, так как этим приемом проблема может быть решена не всегда. Я добавляю только одно замечание, а именно, что, найдя таким методом зависимость между флюэнтами, ты можешь затем согласно проблеме I вернуться к предложенному уравнению, содержащему флюксии, и тогда наверное узнаешь, правильно ли произведено действие или нет.
Предпослав все это беглым образом, я приступаю к общему решению.
Подготовление к решению.
Прежде всего следует заметить, что в предложенном уравнении знаки флюксий в отдельных членах должны быть одинакового измерения (ибо флюксии суть величины иного рода, чем те, для которых они служат флюксиями)»
Речь идет о том, что уравнение должно быть однородным, т. е. все его слагаемые должны измеряться в одних и тех же единицах измерения. Во времена Ньютона выражение вида x 2 + x считалось неправильным, поскольку нельзя "складывать площадь и длину"
«Если в каком-либо случае дело обстоит иначе, то флюксию какой-либо флюэнты следует принять за единицу и помножить на нее низшие члены столько раз, сколько требуется для того, чтобы знаки флюксий привелись во всех членах к одинаковому числу измерений. Уравнения, которые содержат только флюэнты, имеющие везде одинаковое число измерений, всегда можно привести к такому виду, чтобы в одной части находилось отношение флюксий (например, 
или 
или 
и т. д.), а в другой значение этого отношения, выраженное в простых алгебраических членах (таким образом, левая часть уравнения будет зависеть от производной y по x ), как, например,
|
В том случае, когда не может быть применено приведенное выше частное решение, уравнения всегда следует представлять в этой форме.
Поэтому, когда в значении этого отношения имеется какой-либо член с составным знаменателем или радикалом или когда это отношение представляет собой корень неявного уравнения, то прежде чем приступить к действиям, ты должен совершить приведение либо посредством деления, либо с помощью извлечения корня, либо с помощью решения неявного уравнения, как мы это объясняли выше.»
Речь идет, по существу, о хорошо известном методе Ньютона решения нелинейных уравнений, описываемом Ньютоном в предыдущем разделе трактата в форме представления решений в виде ряда.
«Пусть, например, предложено уравнение
Прежде всего приведение его дает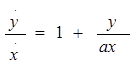 
или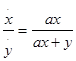 
При первом предположении я обращаю выражение y /(a x ), у которого знаменатель есть составное выражение a x , в бесконечный ряд простых членов: 
(приведение это производятся делением числителя y на знаменатель a x ), откуда получаю 