Реферат: Теория флюксий
Таким же образом, если данное уравнение есть
или
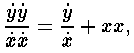
или после дальнейшего преобразования
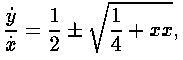
то я извлекаю квадратный корень из членов 1 /4 +xx и получаю бесконечный ряд
|
При подстановке его вместо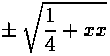 
я буду иметь
|
= 1 + xx x 4 +2x 7 5x 8 + 14x 10 и т. д.или
|
смотря по тому, прибавляю ли 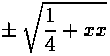к 1 /2 или вычитаю из нее.»
В этих примерах Ньютон описывает первый этап своего метод решения дифференциальных уравнений. В современной терминологии это приведение уравнения к нормальной форме и разложение правой части в степенной ряд.
«Далее, чтобы легче было отличать одну из флюэнт от других, можно с достаточным основанием ту из флюксий, которая находится в числителе отношения, назвать величиной отнесенной, а ту, которая стоит в знаменателе и с которой сравнивается первая, соотнесенной, -зависимая и, соответственно, независимая переменные в дифференциальном уравнении; и этими же терминами можно соответственно называть и флюэнты. Для лучшего понимания дальнейшего можно представлять себе, что соотнесенная величина есть время или, лучше, какая-либо равномерно текущая величина, с помощью которой выражается и измеряется время, а другая, именно отнесенная, величина есть пространство, проходимое за это время вещью или точкой, обладающей некоторым ускоренным или замедленным движением. Сущность проблемы заключается тогда в определении пройденного за все время пути, если известна скорость для любого момента времени.»
Классификация уравнений в рамках проблемы и их решение
Уравнения, относящиеся к этой проблеме, Ньютон разделил на три рода:
1. уравнения вида F (x ,
,
) = 0, приводящиеся к виду f (x ,dy /dx ) = 0 «…те уравнения, в которых имеются две флюксии величин и только одна из флюэнт».
2. уравнения вида F (x ,y ,,) = 0, приводящиеся к виду f (x , y , dy /dx ) = 0. «…те, которые содержат обе текущие величины с их флюксиями.»
3. Одно дифференциальное уравнение с несколькими неизвестными. «…те, в которых имеются флюксии больше чем двух величин»
Ньютон рассматривает и решение каждого из случаев.
Решение первого случая.
«Прими единственную имеющуюся в уравнению флюэнту за соотнесенную величину и, преобразовав уравнение в соответствии с этим допущением (т. е. установив отношение флюксии второй величины к флюксии первой и значение этого отношения, выраженного через простые члены(Т. е. разложенного в степенной ряд)), помножь значение отношения флюксий на соотнесенную величину. Затем раздели каждый член этого выражения на показатель степени, в которую возведена в нем соотнесенная величина; то что ты таким образом получишь, и будет равно другой текущей величине.»
В современных терминах это выглядит так: нужно уравнение f (x , y ) = 0 привести к виду y’ =j (x ) и проинтегрировать. Процедура же интегрирования сводится к разложениюj в степенной ряд и последующему почленному интегрированию ряда.
Решение второго случая.
«До сих пор речь шла об уравнениях, которые заключают одну флюэнту. Когда же в уравнении появляются обе, то уравнение прежде всего следует привести к уже указанному виду, полагая с одной стороны отношение флюксий, а с другой равную ему сумму простых членов.
Кроме того, если какой-либо член преобразованного таким образом уравнения представляет дробь с флюэнтой в знаменателе, то он должен быть освобожден от подобного знаменателя при помощи вышеприведенной замены текущей величины.
Таким образом, если дано уравнение
или 