Реферат: Теория игр
Оптимальные стратегии для игрока 2 можно найти из системы
и, следовательно, Y = (0; 
; 
). (Из рисунка видно, что стратегия B1 не войдёт в оптимальную стратегию.
Пример 2 . Найти решение игры, заданной матрицей
|
x 8
|
7
|
|
6 К 6
|
|
4
|
2
|
|
|
y
Решение . Матрица имеет размерность 2 х 4. Строим прямые, соответствующие стратегиям игрока 1. Ломанная А1 K А¢4 соответствует верхней границе выигрыша игрока 1, а отрезок NK –цене игры. Решение игры таково
U = (
; 
); Х = (
; 0; 0; 
); u = 
.
Сведение матричной игры к задаче линейного программирования
Предположим, что цена игры положительна (u > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с , прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются .
Итак, пусть дана матричная игра с матрицей А порядка mх n. Согласно свойству 7 оптимальные смешанные стратегии х = (х1 , ..., х m ), y = (y1 , ..., yn ) соответственно игроков 1 и 2 и цена игры u должны удовлетворять соотношениям.
Разделим все уравнения и неравенства в (1) и (2) на u (это можно сделать, т.к. по предположению u > 0) и введём обозначения :
, 
,
Тогда (1) и (2) перепишется в виде :
, 
, 
, ,
, 
, 
, .
Поскольку первый игрок стремится найти такие значения х i и, следовательно, pi , чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений pi , при которых
, . 
Поскольку второй игрок стремится найти такие значения yj и, следовательно, qj , чтобы цена игры u была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj , , при которых
, . 
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).
Решив эти задачи, получим значения pi , qj и u .Тогда смешанные стратегии, т.е. xi и yj получаются по формулам :
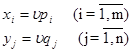
Пример . Найти решение игры, определяемой матрицей.