Реферат: Теплоёмкость. Термодинамические процессы с идеальным газом

P1×v1×ln(P1/P2)

T×ΔS = R×T×ln(V2/V1) адиабатный –Δu = (P1×v1 – P2×v2) /(k – 1) 0

Теплоёмкость при политропном процессе равна:

(5.1)

На рисунке ниже приведены политропные процессы в P – V и T – S координатах.

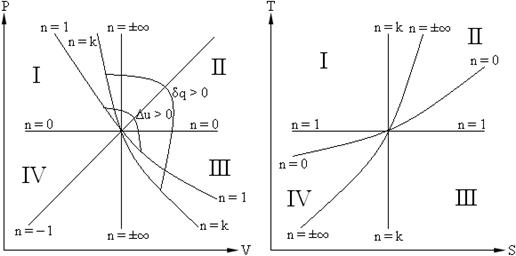
Рис. 2.1

Пример. Воздух, имеющий объем V = 0,01 м3, при Р1 = 10 бар и Т1 = = 298 К расширяется в цилиндре с подвижным поршнем до давления Р2 = 1 бар. Определить конечный объем, температуру, работу расширения, подведенное тепло, изменение внутренней энергии, энтальпии и энтропии, если расширение происходит: 1. изотермически; 2. адиабатически; 3. политропно с показателем политропы n = 1,3. Изобразить процесс в P – V и T – S координатах.

Решение:

Изотермическое расширение.

Объем в конце расширения:

V2 = V1 × (P1/P2) = 0,01 × (10/1) = 0,1 м3.

Работа расширения:

L = P1 × V1 × ln(P1/P2) = 106 × 0,01 × ln(10/1) = 23 кДж.

Количество подведенного тепла:

QT = L = 23 кДж.

Так как Т1 = Т2 = 298 К, то Δh = 0 и Δu = 0.

Изменение энтропии:

ΔS = Q/T = 23/298 = 0,07718 кДж/К.

Адиабатное расширение.

Масса газа в цилиндре:

m = (P1 × V1 × μ) /R × T1 = (106 × 0,01 × 2,896×10–2) /(8,314 × 298 К) = 0,117 кг.

Конечный объем:

V2 = V1 × (P1/P2) 1/k = 0,01 × (10/1) 1/1,4 = 0,0518 м3.

Температура воздуха в конце процесса:

T2 = T1 × (P2/P1) (k – 1) /k = 298 × (1/10) (1,4 – 1) /1,4 = 154,35 К.

Работа газа при расширении:

L = (P1 × V1 – P2 × V2) /(k – 1) = (106 × 0,01 – 105 × 0,0518) /(1,4 – 1) = 12 кДж.

Изменение в процессе составило:

Энтальпии: