Реферат: Термодинамические потенциалы

Из последнего равенства понятно, почему энтальпию еще называют теплосодержанием. При горении и других химических реакциях, происходящих при постоянном давлении (), выделяемое количество теплоты равно изменению энтальпии.

Выражение (3.11), с учетом второго начала термодинамики (2.7) позволяет определить теплоемкость:

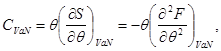
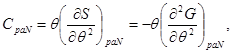
(3.12)

Все термодинамические потенциалы типа энергии обладают свойством аддитивности. Поэтому можно записать:

(3.13)

Легко видеть, что потенциал Гиббса содержит только один аддитивный параметр , т.е. удельный потенциал Гиббса от не зависит. Тогда из (3.4) следует:

(3.14)

То есть химический потенциал есть удельный потенциал Гиббса, и имеет место равенство

(3.15)

Термодинамические потенциалы (3.1) связаны между собой прямыми соотношениями, позволяющими совершать переход от одних потенциалов к другим. Например, выразим все термодинамические потенциалы через внутреннюю энергию.

(3.16)

При этом мы получили все термодинамические потенциалы как функции (). Для того, чтобы выразить их в других переменных, используют процедуру пере….

Пусть задано давление в переменных ():

(3.17)

Запишем последнее выражение в виде уравнения состояния, т.е. найдем вид

Легко видеть, что если состояние задано в переменных (), то термодинамическим потенциалом является внутренняя энергия В силу (3.2) найдем

(3.18)

Рассматривая (3.18) как уравнение относительно S, находим его решение:

(3.19)

Подставляя (3.19) в (3.17) получаем

(3.20)

То есть от переменных () мы перешли к переменным ().

2.

Вторая группа термодинамических потенциалов возникает в том случае, если в качестве термодинамических переменных, помимо рассмотренных выше, включен химический потенциал . Потенциалы второй группы также имеют размерность энергии и могут быть связаны с потенциалами первой группы путем соотношений:

(3.21)

Соответственно дифференциалы потенциалов (3.21) имеют вид:

(3.22а)

(3.22б)

(3.22в)

(3.22г)

Также как и для термодинамических потенциалов первой группы, для потенциалов (3.21) можно построить термодинамические тождества, найти выражения параметров термодинамической системы и т.д.

Рассмотрим характерные соотношения для “потенциала омега” , выражающий квазисвободную энергию, и использующийся на практике наиболее часто среди остальных потенциалов группы (3.22).

Потенциал задается в переменных (), описывающих термодинамическую систему с воображаемыми стенками. Параметры системы в этом случае определяются из соотношений:

(3.23)

Термодинамические тождества, следующие из потенциальности , имеют вид:

(3.24)

Достаточно интересными являются аддитивные свойства термодинамических потенциалов второй группы. Поскольку в этом случае число частиц не входит в число параметров системы, то в качестве аддитивного параметра используют объем. Тогда для потенциала получаем:

(3.25)

Здесь - удельный потенциал на 1. Учитывая (3.23), получаем:

, соответственно, (3.26)

Справедливость (3.26) можно доказать и на основе (3.15):