Реферат: Термодинамические потенциалы

Вычислим производные и и подставим их в последнее выражение:

Тогда

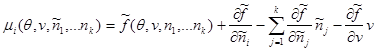(3.42)

Выражение для давления, напротив упростится:

(3.43)

Аналогичные соотношения могут быть получены и для потенциала Гиббса. Так, если в качестве аддитивного параметра задан объем, то с учетом (3.37) и (3.38) запишем:

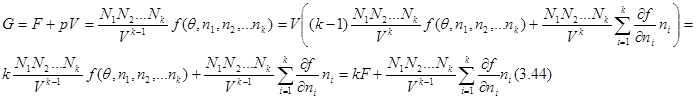это же выражение может быть получено из (3.юю), которое в случае многих частиц принимает вид:

(3.45)

Подставляя в (3.45) выражение(3.39), находим:

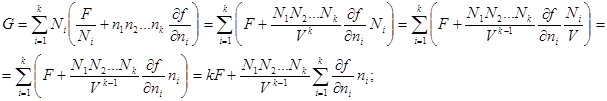
что полностью совпадает с (3.44).

Для того, чтобы перейти к традиционной записи потенциала Гиббса (через переменные состояния ()) необходимо разрешить уравнение (3.38):

Относительно объема V и подставить результат в (3.44) или (3.45):

Если в качестве аддитивного параметра задано полное число частиц в системе N, то потенциал Гиббса с учетом (3.42) принимает следующий вид:

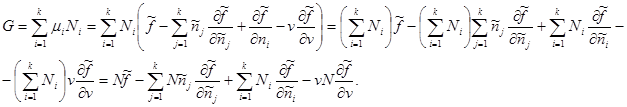
Зная вид удельных величин: ,получим:

.

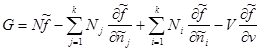В последнем выражении суммирование по j заменим на суммирование по i . Тогда второе и третье слагаемые в сумме дают нуль. Тогда для потенциала Гиббса окончательно получим:

. (3.46)

Это же соотношение может быть получено и другим способом (из (3.41) и (3.43)):

Далее рассмотрим многокомпонентную систему “под поршнем”, состояние которой описывается параметрами (). Роль термодинамического потенциала в этом случае играет потенциал Гиббса:

(3.47)

Тогда для химического потенциала каждой из компонент получим:

(3.48)

При выводе (3.48) выполнены преобразования, аналогичные использованным при выводе (3.42), с помощью воображаемых стенок. Параметры состояния системы образуют набор ().

Роль термодинамического потенциала играет потенциал , который принимает вид:

(3.49)

Как видно из (3.49), единственным аддитивным параметром в данном случае является объем системы V.

Определим некоторые термодинамические параметры такой системы. Число частиц в данном случае определяется из соотношения:

(3.50)

Для свободной энергии F и потенциала Гиббса G можно записать:

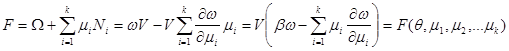(3.51)

(3.52)

Таким образом, соотношения для термодинамических потенциалов и параметров в случае многокомпонентных систем видоизменяются только за счет необходимости учета числа частиц (или химических потенциалов) каждой компоненты. При этом сама идея метода термодинамических потенциалов и расчетов, проводимых на его основе, остается неизменной.

4.

В качестве примера использования метода термодинамических потенциалов рассмотрим задачу химического равновесия. Найдем условия химического равновесия в смеси трех веществ, вступающих реакцию. Дополнительно предположим, что исходные продукты реакции является разреженными газами(это позволяет не учитывать межмолекулярные взаимодобывания), а в системе поддерживаются постоянные температура и давление , (такой процесс наиболее просто реализовать практически, поэтому условие постоянства давления и температуры создаются в промышленных установках для химической реакции ).

Условие равновесия термодинамической системы в зависимости от способа ее описания определяются максимальной энтропией системы или минимальной энергией системы (подробнее см. Базаров Термодинамика). Тогда можно получить следующие условия равновесия системы:

1. Состояние равновесия адиабатически изолированной термодинамической системы, заданной параметрами (), характеризуется максимумом энтропии:

(3.53а)

Второе выражение в (3.53а) характеризует устойчивость равновесного состояния.

2. Состояние равновесия изохорно-изотермической системы, заданное параметрами (), характеризуется минимумом свободной энергии. Условие равновесия в этом случае принимает вид:

(3.53б)

3. Равновесие изобарно-изотермической системы, задаваемой параметрами (), характеризуется условиями:

(3.53в)