Реферат: Туннелирование в микроэлектронике
введя обозначение:
![]() , (1.4)
, (1.4)
окончательно получим:
![]() (1.5).
(1.5).
Аналогично для области II:
![]() , (1.6)
, (1.6)
где ![]()
![]() . Таким образом, мы получили характеристические уравнения, общие решения которых имеют вид:
. Таким образом, мы получили характеристические уравнения, общие решения которых имеют вид:
![]() при x<0, (1.7)
при x<0, (1.7)
![]() при x>0 (1.8)
при x>0 (1.8)
Слагаемое ![]() соответствует волне, распространяющейся в области I в направлении оси х, А1 - амплитуда этой волны. Слагаемое
соответствует волне, распространяющейся в области I в направлении оси х, А1 - амплитуда этой волны. Слагаемое ![]() соответствует волне, распространяющейся в области I в направлении, противоположном х. Это волна, отражённая от барьера, В1 - амплитуда этой волны. Так как вероятность нахождения микрочастицы в том или ином месте пространства пропорциональна квадрату амплитуды волны де Бройля, то отношение
соответствует волне, распространяющейся в области I в направлении, противоположном х. Это волна, отражённая от барьера, В1 - амплитуда этой волны. Так как вероятность нахождения микрочастицы в том или ином месте пространства пропорциональна квадрату амплитуды волны де Бройля, то отношение  представляет собой коэффициент отражения микрочастицы от барьера.
представляет собой коэффициент отражения микрочастицы от барьера.
Слагаемое ![]() соответствует волне, распространяющейся в области II в направлении х. Квадрат амплитуды этой волны отражает вероятность проникновения микрочастицы в область II. Отношение
соответствует волне, распространяющейся в области II в направлении х. Квадрат амплитуды этой волны отражает вероятность проникновения микрочастицы в область II. Отношение  представляет собой коэффициент прозрачности барьера.
представляет собой коэффициент прозрачности барьера.
Слагаемое ![]() должно соответствовать отражённой волне, распространяющейся в области II. Так как такой волны нет, то В2 следует положить равным нулю.
должно соответствовать отражённой волне, распространяющейся в области II. Так как такой волны нет, то В2 следует положить равным нулю.
Для барьера, высота которого U>E, волновой вектор k2 является мнимым. Положим его равным ik, где ![]() является действительным числом. Тогда волновые функции
является действительным числом. Тогда волновые функции ![]() и
и ![]() приобретут следующий вид:
приобретут следующий вид:![]()
![]() (1.9)
(1.9)
![]() (1.10)
(1.10)
Так как ![]() , то это значит, что имеется вероятность проникновения микрочастицы на некоторую глубину во вторую область. Эта вероятность пропорциональна квадрату модуля волновой функции
, то это значит, что имеется вероятность проникновения микрочастицы на некоторую глубину во вторую область. Эта вероятность пропорциональна квадрату модуля волновой функции ![]() :
:
![]() . (1.11)
. (1.11)
Наличие этой вероятности делает возможным прохождение микрочастиц сквозь потенциальный барьер конечной толщины l (рис. 1.1). Такое просачивание получило название туннельного эффекта. По формуле (1.11) коэффициент прозрачности такого барьера будет равен:
![]() , (1.12)
, (1.12)
где D0 – коэффициент пропорциональности, зависящий от формы барьера. Особенностью туннельного эффекта является то, что при туннельном просачивании сквозь потенциальный барьер энергия микрочастиц не меняется: они покидают барьер с той же энергией, с какой в него входят.
Туннельный эффект играет большую роль в электронных приборах. Он обуславливает протекание таких явлений, как эмиссия электронов под действием сильного поля, прохождение тока через диэлектрические плёнки, пробой p-n перехода; на его основе созданы туннельные диоды, разрабатываются активные плёночные элементы.
2.1 КОНТАКТ МЕТАЛЛ-МЕТАЛЛ
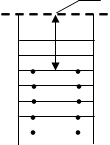
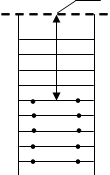
Рассмотрим плотный контакт двух металлов М1 и М2 с разными работами выхода А1 и А2 (рис. 2.1.1).
A1 A2
 |  |
EF1 n21
![]()
n12 EF2
![]()
![]() d
d
M1 M2
Рис. 2.1.1 Энергетическая диаграмма контакта двух металлов в начальный момент времени
Вследствие того, что уровень Ферми EF 1 в М1 (уровень Ферми это то значение энергии уровня, выше которого значения энергии электрон принимать не может при Т=0 К) находится выше, чем EF 2 в М2 , соответствующие работы выхода А1 <А2 . Если Т![]() 0 К, то при контакте металлов между ними начнётся обмен электронами за счёт термоэлектронной эмиссии. При Т=0 К электроны за счёт туннелирования будут переходить из М1 в М2, так как напротив заполненных уровней в М1 будут находиться свободные уровни в М2 .
0 К, то при контакте металлов между ними начнётся обмен электронами за счёт термоэлектронной эмиссии. При Т=0 К электроны за счёт туннелирования будут переходить из М1 в М2, так как напротив заполненных уровней в М1 будут находиться свободные уровни в М2 .