Реферат: Туннелирование в микроэлектронике

Если току и напряжению приписывать положительный знак, когда они направлены слева направо, то выражение (2.1.7) для результирующего тока примет такой же вид, как и выражение (2.1.9). Поэтому выражение (2.1.9) называют уравнением вольтамперной характеристики контакта двух металлов.

Из выражения (2.1.9) видно, что контакт металл-металл обладает выпрямляющим действием. При V>0 ток увеличивается по экспоненте, а при V<0 –уменьшается.

В обычных условиях контакт металл-металл является невыпрямляющим, так как при плотном контакте, толщина возникающего потенциального барьера –qV_k очень мала, и он будет прозрачен для туннельного просачивания электронов. Если же ширина зазора между металлами каким-либо образом увеличится, то туннельный эффект можно исключить и все полученные выводы будут справедливы.

Проблема электрического контакта двух металлов представляется особенно существенной в микроэлектронике. Это обусловлено тем, что в микроэлектронных устройствах используются рабочие напряжения, близкие по величине к контактным разностям потенциалов.

2.2 СТРУКТУРА МЕТАЛЛ-ДИЭЛЕКТРИК-МЕТАЛЛ

Туннельный механизм прохождения электронов сквозь тонкие диэлектрические слои может проявляться и быть преобладающим
при малой концентрации носителей тока в плёнке диэлектрика, сравнительно высоких барьерах на поверхности диэлектрика, низких температурах и достаточно малых, толщинах плёнки. Резуль­тирующий
туннельный ток из одного электрода в другой сквозь диэлектрический
слой находится как раз­ность встречных туннельных составляющих
токов в направлении х, перпендикулярном плоскости плёнки. Со­ставляющие этой разности определяют интегрированием произведения
концентрации электронов в электродах на прозрачность барьера по
всем значениям энергии электронов. Полученное таким образом уравне­ние для туннельного тока имеет вид:

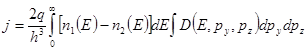, (2.2.1)

где n₁ (Е) и n₂ (Е)- концентрации электронов с энергиями от Е до Е+dE в первом и втором электродах соответ­ственно; D(Е, p_y , p_z )- вероятность проникновения электрона с энергией Е сквозь
потенциальный барьер (про­зрачность барьера), h- постоянная
Планка, р_y , р_z ,- компоненты импульса электрона в плоскости, параллельной плоскости плёнки.

Зоммерфельдом А. И Бете Г. был рассчитан туннельный ток
сквозь вакуумный зазор между двумя одинако­выми металлическими
электродами (прямоугольный потенциальный барьер). Вольт-амперная
характери­стика системы при малых напряжениях имеет вид:

, (2.2.2)

и при больших напряжениях (qu>+E_F ):

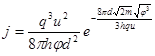, (2.2.3)

где - высота потенциального барьера; d- ширина зазора; u- -
приложенное напряжение; m- масса электрона. Из полученных
выражений видно, что при малых напряжениях характеристика
линейна, а при увеличении на­пряжения ток резко возрастает.

Однако реальный барьер имеет более сложную форму. Поэтому
детальный расчёт вольт-амперной характери­стики должен производиться с учётом сил изображения, различия эффективных масс носителей заряда в металле и диэлектрике, а также с учётом пространственного заряда электронов, тун­нелировавших из металла в зону проводимости диэлектрика, и электронов, попавших на ловушки в диэлектрике. Симмонсом Дж. был предложен метод расчёта туннельного тока для барьера произ­вольной формы. Он ввёл понятие о барьере средней величины. Этот метод принципиально позво­ляет вычислить туннельный ток с учётом названных факторов, однако при этом получаются очень громоздкие выражения. Анализ результатов расчёта по методу Симмонса показывает, что при малых напряжениях вольтамперная характеристика является линейной, а при больших напряжениях пере­ходит в экспоненциальную зависимость. При дальнейшем увеличении напряжения туннельный ток ограничивается пространственным зарядом в диэлектрике. На рис. 2.2.1 показаны расчётные вольт-амперные характеристики с учётом пространственного заряда.

Из рисунка видно, что большой про­странственный заряд может сильно ограничивать туннельный ток сквозь слой диэлектрика. Большое количество экспериментальных работ было вы­полнено по изучению туннельного прохождения электронов сквозь тонкие диэлектрические слои. Плёнки диэлектриков обычно создавались либо термическим окислением металлов, либо распыле­нием в вакууме. Исследованию были подвергнуты плёнки Al₂ O_3, Ta₂ O₅ , TiO₂ , Сu₂ O, Сu₂ S, SiO, GeO₂ , и других соединений. Практически во всех системах наблюдалось качественное совпадение экспериментальных вольт-амперных характеристик с расчётными. В начале имеет место линейное возрастание тока с ростом напряжения, затем оно пе­реходит в экспоненциальное с последующим замедлением роста тока. Последнее обстоятельство, как и предполагалось при теоретическом рас­чёте, вызвано ловушками в диэлектрических слоях. При соответствующем подборе высоты контакт­ного барьера, эффективной площади структуры, эффек­тивной массы электрона в диэлектрике и дру­гих параметров наблюдается количественное совпаде­ние. На рис. 2.2.2 приведена вольт-амперная ха­рактеристика туннельного тока сквозь слой А1₂ О₃ тол­щиной d=2,3 нм. Точками показаны экспериментальные результаты, сплошной линией – расчётные. Наблюдаемые в отдельных случаях количественные расхождения в теоритических и экспериментальных результах вызваны, по-видимому, несовершенством структуры и геометрии плёнок.

j, а/см²

10⁷ 1

2

10³ 3

10^-1

10^-5

10^-9

1 10 100 1000 u, B

Рис. 2.2.1 Расчётные вольт-амперные характеристики туннельного тока:

1 – без учёта пространственного заряда;

2 – с учётом пространственного заряда подвижных носителей;

3 – с учётом пространственного заряда на ловушках при большой их плотности.

j, а/см²

1

10^-1

10^-2