Реферат: Уравнение Кортевега - де Фриса, солитон, уединенная волна

Открытия, связанные с уравнением Кортевега - де Фриса, не закончились открытием солитона. Следующим важным шагом, имеющим отношение к этому замечательному уравнению, было создание нового метода решения нелинейных уравнений в частных производных. Хорошо известно, что най­ти решения нелинейных уравнений очень сложно. До 60-х годов нашего столетия считалось, что такие уравнения могут иметь только некоторые частные решения, удовлетворяющие специально заданным начальным условиям. Однако уравнение Кортевега—де Фриса и в этом случае оказалось в исключи­тельном положении.

В 1967 году американские физики К.С. Гарднер, Дж.М. Грин, М. Крускал и Р. Миура показали, что решение уравнения Кортевега—де Фриса может быть в принципе получено для всех начальных усло­вий, которые определенным образом обращаются в нуль при стремлении координаты к бесконечности. Они использовали преобразование уравнения Кортевега - де Фриса к системе двух уравнений, называ­емой теперь парой Лакса (по имени американского математика Питера Лакса, внесшего большой вклад в развитие теории солитонов), и открыли новый ме­тод решения ряда очень важных нелинейных урав­нений в частных производных. Этот метод получил название метода обратной задачи рассеяния, по­скольку в нем существенно используется решение задачи квантовой механики о восстановлении по­тенциала по данным рассеяния.

2.2. Групповой солитон

Выше мы говорили, что на практике волны, как правило, распространяются группами. Подобные группы волн на воде люди наблюдали с незапамят­ных времен. На вопрос о том, почему для волн на воде так типичны "стаи" волн, удалось ответить Т. Бенжамену и Дж. Фейеру только в 1967 году. Тео­ретическими расчетами они показали, что простая периодическая волна на глубокой воде неустойчива (теперь это явление называется неустойчивостью Бенжамена—Фейера), и поэтому волны на воде из-за неустойчивости разбиваются на группы. Уравнение, с помощью которого описывается распространение групп волн на воде, было получено В.Е. Захаровым в 1968 году. К тому времени это уравнение уже было известно в физике и носило название нелинейного уравнения Шрёдингера. В 1971 году В.Е. Захаров и А.Б. Шабат показали, что это нелинейное уравне­ние имеет решения также в виде солитонов, более того, нелинейное уравнение Шрёдингера, так же как и уравнение Кортевега—де Фриса, может быть проинтегрировано методом обратной задачи рассея­ния. Солитоны нелинейного уравнения Шрёдинге­ра отличаются от обсуждаемых выше солитонов Кортевега—де Фриса тем, что они соответствуют форме огибающей группы волн. Внешне они на­поминают модулированные радиоволны. Эти солитоны называются групповыми солитонами, а иногда солитонами огибающей. Это название от­ражает сохраняемость при взаимодействии огиба­ющей волнового пакета (аналог штриховой ли­нии, представленной на рис. 3), хотя сами волны под огибающей двигаются со скоростью, отличной от групповой. При этом форма огибающей описывается

Рис. 3. Пример группового солитона (штриховая линия)

зависимостью

a(x,t)=a₀ ch^-1 ()

где а_а - амплитуда, а l — половина размера солитона. Обычно под огибающей солитона находится от 14 до 20 волн, причем средняя волна самая большая. С этим связан хорошо известный факт, что самая вы­сокая волна в группе на воде находится между седь­мой и десятой (девятый вал). Если в группе волн об­разовалось большее количество волн, то произойдет ее распад на несколько групп.

Нелинейное уравнение Шрёдингера, как и урав­нение Кортевега— де Фриса, также имеет широкую распространенность при описании волн в различ­ных областях физики. Это уравнение было предло­жено в 1926 году выдающимся австрийским физи­ком Э. Шрёдингером для анализа фундаментальных свойств квантовых систем [4] и первоначально ис­пользовано при описании взаимодействия внут­риатомных частиц. Обобщенное или нелинейное уравнение Шрёдингера описывает совокупность явлений в физике волновых процессов. Например, оно используется для описания эффекта самофоку­сировки при воздействии мощного лазерного луча на нелинейную диэлектрическую среду и для опи­сания распространения нелинейных волн в плазме.

3. Постановка задачи

3.1. Описание модели.В настоящее время наблюдается значи­тельно возрастающий интерес к исследованию нелинейных волно­вых процессов в различных областях физики (например, в оптике, физике плазмы, радиофизике, гидродинамике и т.д.). Для изучения волн малой, но конечной амплитуды в дисперсионных средах в каче­стве модельного уравнения часто используют уравнение Кортевега-де Фриза (КдФ):

u _t + ии_х + b и_ххх = 0 (3.1)

Уравнение КдФ было использовано для описания магнитозвуковых волн, распространяющихся строго поперек магнитного поля или под углами, близкими к .

Основные предположения, которые делаются при выводе уравне­ния: 1) малая, но конечная амплитуда, 2) длина волны велика по сравнению с длиной дисперсии.

Компенсируя действие нелинейности, дисперсия дает возможность формироваться в дисперсионной среде стационарным волнам конеч­ной амплитуды - уединенным и периодическим. Уединенные волны для уравнения КдФ после работы [8] стали называться солитонами [9]. Периодические волны носят название кноидальных волн. Соот­ветствующие формулы для их описания даны в [4].

3.2. Постановка дифференциальной задачи.В работе иссле­дуется численное решение задачи Коши для уравнения Кортевега-де Фриза с периодическими условиями по пространству в прямоуголь­нике Q_T ={( t , x ):0< t < T , x Î [0, l ].

u _t + ии_х + b и_ххх = 0 (3.2)

u(x,t)|_x=0 =u(x,t)|_x=l (3.3)

с начальным условием

u(x,t)|_t=0 =u₀ (x) (3.4)

4. Свойства уравнения Кортевега - де Фриза

4.1. Краткий обзор результатов по уравнению КдФ.Задача Коши для уравнения КдФ при различных предположениях отно­сительно u ₀ (х) рассматривалась во многих работах [10-17]. Задача о существовании и единственности решения с условиями периодично­сти в качестве краевых условий была решена в работе [10] с помощью метода конечных разностей. Позже, при менее сильных предположе­ниях, существование и единственность были доказана в статье [11] в пространстве L^¥ (0,T,H^s (R¹ )), где s>3/2, а в случае периодической задачи - в пространстве L^¥ (0,T,H^¥ (C))где С - окружность дли­ны, равной периоду, на русском языке эти результаты представлены в книге [12].

Случай, когда не предполагается какая-либо гладкость началь­ной функции u ₀ Î L ₂ ( R ¹ ) , рассмотрен в работе [13]. Там вводит­ся понятие обобщенного решения задачи (3.2),(3.4), устанавливает­ся существование обобщенного решения и( t ,х) Î L ^¥ (0, T , L ² ( R ¹ )) в случае произвольной начальной функции u₀ Î L ₂ ( R ¹ ) ; при этом и( t ,х) Î L ² (0,Т;H^-1 (- r , r )) для любого r>0 , и если для некото­рого a > 0 ( x ^a u ₀ ² ( x )) Î L ¹ (0,+ ¥ ) , то

(4.1)

Используя обращение линейной части уравнения при помощи фун­даментального решения G (t,x) соответствующего линейного опера­тора , вводится класс корректности задачи (3.2),(1.4) и уста­навливаются теоремы единственности и непрерывной зависимости решений этой задачи от начальных данных. Также исследуются во­просы регулярности обобщенных решений. Одним из основных ре­зультатов является достаточное условие существования непрерыв­ной по Гельдеру при t > 0 производной в терминах существования моментов для начальной функции, для любых k и l .

Задача Коши для уравнения КдФ исследовалась также методом обратной задачи рассеяния, предложенном в работе [14]. При по­мощи этого метода были получены результаты о существовании и гладкости решений при достаточно быстро убывающих начальных функциях, причем в [15] установлен, в частности, результат о раз­решимости задачи (3.2),(3.4) в пространстве C ^¥ (О, Т; S(R¹ )) .

Наиболее полный обзор современных результатов по уравнению КдФ можно найти в [16].

4.2. Законы сохранения для уравнения КдФ. Как известно, для уравнения КдФ существует бесконечное число законов сохране­ния. В работе [17] приводится строгое доказательство этого факта. В работах [11], [12] различные законы сохранения применялись для до­казательства нелокальных теорем существования решения задачи (3.2),(3.4) из соответствующих пространств.

Продемонстрируем вывод первых трех законов сохранения для за­дачи Коши на R¹ и периодической задачи.

Для получения первого закона сохранения достаточно проинте­грировать уравнения (3.2) по пространственной переменной. Полу­чим:

отсюда и следует первый закон сохранения:

Здесь в качестве a и b выступают +¥ и -¥ для задачи Коши и границы основного периода для периодической задачи. Поэтому второе и третье слагаемые обращаются в 0.

(4.2)

Для вывода второго закона сохранения следует умножить уравне­ние (3.2) на 2 u (t,x) и проинтегрировать по пространственной пере­менной. Тогда, используя формулу интегрирования по частям полу­чим:

но в силу "краевых" условий все слагаемые кроме первого опять сокращаются

Таким образом второй интегральный закон сохранения имеет вид:

(4.3)

Для вывода третьего закона сохранения нужно умножить наше уравнение (3.2) на (и² + 2 b и_хх ), таким образом получим:

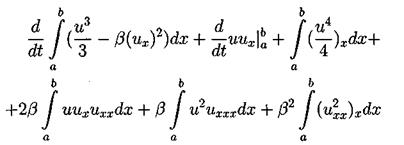
После применения несколько раз интегрирования по частям тре­тий и четвертый интегралы сокращаются. Второе и третье слагае­мые исчезают из-за граничных условий. Таким образом из первого интеграла получаем:

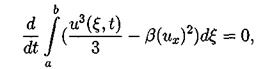
что эквивалентно