Реферат: Уравнение Кортевега - де Фриса, солитон, уединенная волна

А это и есть третий закон сохранения для уравнения (3.2). Под физическим смыслом первых двух интегральных законов со­хранения в некоторых моделях можно понимать законы сохранения импульса и энергии, для третьего и последующих законов сохране­ния физический смысл охарактеризовать уже труднее, но с точки зрения математики эти законы дают дополнительную информацию о решении, которая используется потом для доказательств теорем существования и единственности решения, исследования его свойств и вывода априорных оценок.

5. Разностные схемы для решения уравнения КдФ

3.1. Обозначения и постановка разностной задачи. В области ={( x , t ):0 £ x £ l ,0 £ t £ T } обычным образом введем равномерные сетки, где

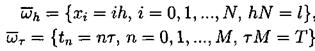
Введем линейное пространство W _h сеточных функций, определен­ных на сетке со значениями в узлах сетки y_i = y^h ( x_i ). Пред­полагается, что выполнены условия периодичности y ₀ = y_N . Кроме того, формально полагаем y_{i + N} = y_i для i ³ 1 .

Введем скалярное произведение в пространстве W _h

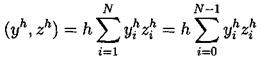(5.1)

Снабдим линейное пространство П/г нормой:

Поскольку в пространство W _h входят периодические функции, то это скалярное произведение эквивалентно скалярному произведе­нию:

Будем строить разностные схемы для уравнения (3.2) на сетке с периодическими краевыми условиями. Нам потребуются обозна­чения разностных аппроксимаций. Введем их.

Используем стандартные обозначения для решения уравнения на очередном (n-м) временном слое, то есть