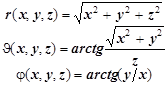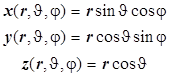Реферат: Уравнение Шрёдингера для простейших стационарных движений
![]() . (6.10)
. (6.10)
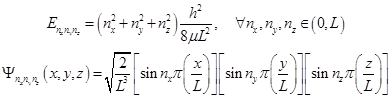 (6.11)
(6.11)
6.6. Пространственное вращение. Общие свойства момента импульса.
При свободном вращении линейной молекулы относительно центра масс потенциальная энергия нулевая. Оператор кинетической энергии следует представить в шаровой системе координат.
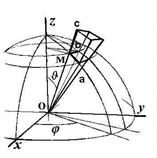
6.6.1. Краткое содержание. Жёсткий ротатор и его уравнение Шрёдингера. Шаровые координаты (r, J, j). Элемент объёма. Лапласиан и уравнение Лапласа в шаровых координатах. Разделение переменных. Роль симметрии в выборе радиальной части общего решения. Радиальная и угловая части уравнения Шрёдингера и вид общего решения. Угловая часть уравнения Лапласа (уравнение Лежандра) и операторное уравнение для момента импульса. Квадрат модуля и проекция на ось вращения в шаровых переменных. Квантование модуля и квантование проекции момента импульса ротатора. Уровни энергии и их вырождение.
|
|
Радиальная переменная r
Угол широты J
Угол долготы j
|
Декартовы координаты:
Элемент объёма в шаровых переменных (см. рис.:
![]() .(6.12)
.(6.12)
Во многих задачах достаточно выделить элемент объёма, не зависящий от направления, и имеющий вид тонкого поверхностного слоя на шаре. В таком случае, избавляясь от угловых аргументов и оставляя лишь радиальную переменную, получаем сферический элемент объёма
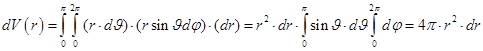 .(6.13)
.(6.13)
6.6.2. Лапласиан. Очень важным свойством лапласиана является его симметрия ко взаимным перестановкам декартовых координат.
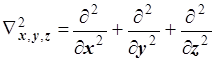 (6.14)
(6.14)
Простейшее дифференциальное уравнение, в котором лапласиан играет основную роль - уравнение Лапласа. Это дифференциальное уравнение в частных производных второго порядка. В различные квантово-механические задачи о сферических системах лапласиан входит в качестве основного оператора. Симметрия конкретной системы предопределяет вид координат, к которым следует преобразовать лапласиан, а далее и вид решений тех дифференциальных уравнений, у которых уравнение Лапласа можно выделить в качестве однородной части. Таковы задачи о сферически симметричных движениях. В шаровых координатах лапласиан оказывается составленным из трёх независимых компонент-операторов, каждый из которых преобразует лишь одну из трёх независимых пространственных переменных.
6.6.3. Перевод лапласиана в шаровые координаты можно осуществить, используя различные схемы. В сферических координатах он выглядит довольно внушительно, но при ближайшем рассмотрении оказывается достаточно простой конструкцией. Несложные, но длительные, преобразования приводят к следующей формуле:
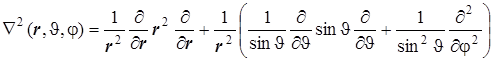 . (6.15)
. (6.15)
Упрощая, выделим вначале операторы чисто радиальный и чисто угловой:
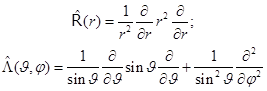 .(6.16)
.(6.16)
6.6.4. Операторные компоненты лапласиана. Первое слагаемое активно только к радиальной переменной, второе же - к угловым аргументам и оно называется оператором Лежандра. Лапласиан получает вид
![]() . (6.17)
. (6.17)
6.6.5 Угловой оператор - оператор Лежандра далее также разделяется на два независимых оператора. Один из них действует на переменную широты J, а второй - на переменную долготы j, так что получается:
![]()
![]() . (6.18)
. (6.18)
6.7. Сферическим уравнением Лапласа назовём дифференциальное уравнение в частных производных второго порядка
![]() .(6.19)
.(6.19)
В сферических переменных оно приобретает вид
![]() , (6.20)
, (6.20)
Решения отыщем по методу Фурье. Для разделения переменных искомое решение представим как произведение радиальной и угловой функций.