Реферат: Уравнение Шрёдингера для простейших стационарных движений

6.7.1. Радиальную часть общего решения сферического уравнения Лапласа выбирают в простейшем виде степенной функции от радиальной переменной, Показатель степени l полагают целочисленным неотрицательным числом . Только в этом случае соблюдается симметрия общего решения по отношению ко взаимным перестановкам декартовых координат, и делается возможно построение регулярных решений (функций класса Q ), (конечных, однозначных и непрерывных), (далее нормированных).

. (6.21)

Угловые сомножители общего решения Y(J,j) называются сферическими гармониками (шаровыми функциями). Запишем уравнение Лапласа, и рассмотрим процедуру разделения переменных:

. (6.22)

Подставим радиальный оператор и совершим следующие простейшие преобразования:

.

Перенесём одно из слагаемых в сторону от знака равенства и разделим обе части на Y(J,j):

.

6.7.2. Итоговое дифференциальное уравнение называется уравнением Лежандра.

Оно включает лишь угловую часть лапласиана и имеет вид:

. (6.23)

Уравнение Лежандра, встречается в нескольких фундаментальных задачах: 1) в задаче о квантовых состояниях и энергетических уровнях ротатора - линейной молекулы, свободно вращающейся вокруг центра массы. 2) в уравнении Шрёдингера для атома H и водородоподобных ионов.

6.7.3. Уравнение Лежандра это вполне типичное операторное уравнение на собственные функции и собственные значения. С точностью до постоянного множителя уравнение Лежандра идентично операторному уравнению на собственные значения для оператора квадрата момента импульса. Напомним вид самого оператора момента импульса:

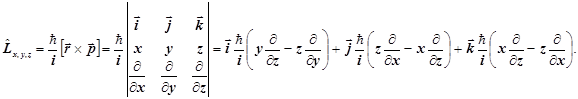
Перенесём постоянный множитель влево, получим

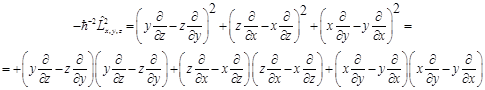(6.24)

6.7.4. Преобразуя оператор слева от знака равенства к шаровым переменным, получаем не что иное, как оператор Лежандра, т.е.:

. (6.25)

На этом основании решения уравнения Лежандра являются решениями также и операторного уравнения на собственные значения квадрата момента импульса. Отсюда строго получается формула для квантования модуля и проекции момента импульса. Это означает

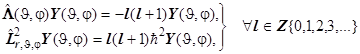. (6.26)

6.7.5. Квадрат модуля момента импульса определяется собственными значениями оператора Лежандра. Допустимые значения модуля момента импульса свободно вращающейся вокруг центра масс квантовой системы (жесткого ротатора) следуют из операторного уравнения (6.25):

. (6.27)

Соответственно при пространственном вращении возможные дискретные значения модуля момента импульса и его проекций на ось вращения определяется двумя формулами

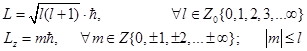(6.28)

6.8. Ротатор. Вращательные состояния ротатора . Углы прецессии момента импульса. Энергетические уровни ротатора непосредственно связаны с квадратом момента.

.(6.29)

Кратность вырождения уровня называется его статистическим весом и определяется как число

возможных состояний с одним и тем же моментом, т.е. равно числу возможных проекций. Статистические веса уровней ротатора g_l равны:

. (6.30)