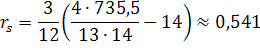Реферат: Установление связи между характеристиками когнитивного развития учащихся и их успешностью в обучении математике
Перед подсчетом коэффициента корреляции убедимся, что между уровнем понятийного мышления учащихся и их учебными достижениями по математике существует определенная связь. Для этого по рангам, полученным учениками, построим диаграмму рассеивания.
Диаграмма показывает, что в целом, несмотря на некоторые отклонения, с увеличением ранга ученика по уровню понятийного мышления увеличивается ранг по успешности в математике, т.е. существует определенная связь. Вычислим коэффициент корреляции.
Коэффициент ранговой корреляции Спирмена вычисляется по формуле:
,
Где 
| ФИ ученика | Кол-во баллов за тест (x) |
Показатель понятийного мышления(y) Кол-во ошибок |  |  |  |  |  |
| Елагин | 23 | 2 | 1 | 1 | 0 | 0 | 1 |
| Калиманов | 18 | 3 | 5,5 | 3 | 2,5 | 6,25 | 16,5 |
| Дольнев | 19 | 3 | 3,5 | 3 | 0,5 | 0,25 | 10,5 |
| Киселёва | 18 | 3 | 5,5 | 3 | 2,5 | 6,25 | 16,5 |
| Фёдорова | 17 | 8 | 7 | 6,5 | 0,5 | 0,25 | 45,5 |
| Богданов | 19 | 9 | 3,5 | 8 | -4,5 | 20,25 | 28 |
| Суббота | 10 | 11 | 10,5 | 10 | 0,5 | 0,25 | 105 |
| Луц | 13 | 8 | 9 | 6,5 | 2,5 | 6,25 | 58,5 |
| Колесников | 20 | 13 | 2 | 11,5 | -9,5 | 90,25 | 23 |
| Мащенко | 10 | 13 | 10,5 | 11,5 | -1 | 1 | 120,75 |
| Коркос | 8 | 10 | 12 | 9 | 3 | 9 | 108 |
| Кладка | 16 | 6 | 8 | 5 | -3 | 9 | 40 |
| ∑ | 149 | 573,25 |
Найденное значение 
является приближенным, поскольку в рассмотренном примере есть так называемые связанные ранги, когда два или более объектов имеют одинаковые показатели и их ранги находятся как средние арифметические соответствующих рангов. В этом случае лучший результат дает применение следующей формулы, которая эквивалентна предыдущей:
Вычислим по предыдущим данным ранговый коэффициент корреляции Спирмена по этой формуле. Имеем:
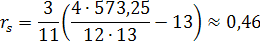
Значение свидетельствует о слабой прямой связи между уровнем понятийного мышления учащихся и их учебными достижениями по математике.
Вычислим для наших данных коэффициент корреляции Пирсона.
| ФИ ученика | Кол-во баллов за тест (x) | Показатель понятийного мышления(y) Кол-во правильных ответов |  |  |  |
| Елагин | 23 | 18 | 529 | 324 | 414 |
| Калиманов | 18 | 17 | 324 | 289 | 306 |
| Дольнев | 19 | 17 | 361 | 289 | 323 |
| Киселёва | 18 | 17 | 324 | 289 | 306 |
| Фёдорова | 17 | 12 | 289 | 144 | 204 |
| Богданов | 19 | 11 | 361 | 121 | 209 |
| Суббота | 10 | 9 | 100 | 81 | 90 |
| Луц | 13 | 12 | 169 | 144 | 156 |
| Колесников | 20 | 7 | 400 | 49 | 140 |
| Мащенко | 10 | 7 | 100 | 49 | 70 |
| Коркос | 8 | 10 | 64 | 100 | 80 |
| Кладка | 16 | 14 | 256 | 196 | 224 |
| ∑ | 191 | 151 | 3277 | 2075 | 2522 |
Коэффициент корреляции Пирсона вычисляется по формуле:
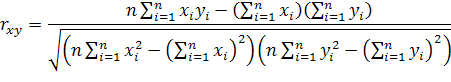
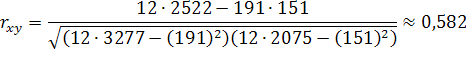
Значение 
свидетельствует о слабой прямой связи между уровнем понятийного мышления учащихся и их учебными достижениями по математике.
Выявление связи между уровнем концентрации внимания учащихся и их учебными достижениями по математике
Применим метод ранговой корреляции Спирмена для нашего исследования.
Перед подсчетом коэффициента корреляции убедимся, что между уровнем концентрации внимания учащихся и их учебными достижениями по математике существует определенная связь. Для этого по рангам, полученным учениками, построим диаграмму рассеивания.
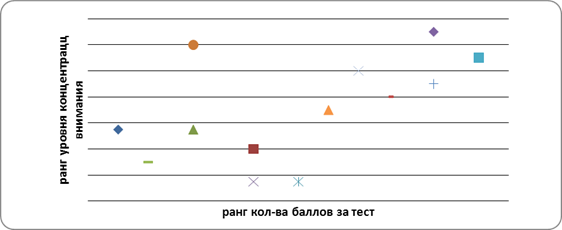
Диаграмма показывает, что несмотря на некоторые отклонения, с увеличением ранга ученика по уровню концентрации внимания увеличивается ранг по успешности в математике, т.е. существует определенная связь. Вычислим коэффициент корреляции Спирмена:
| ФИ ученика | Кол-во баллов за тест (x) | Уровень концентрации внимания | | | | | |
| Елагин | 23 | 73 | 1 | 5,5 | -4,5 | 20,25 | 5,5 |
| Калиманов | 18 | 74 | 5,5 | 4 | 1,5 | 2,25 | 22 |
| Дольнев | 19 | 73 | 3,5 | 5,5 | -2 | 4 | 19,25 |
| Киселёва | 18 | 83 | 5,5 | 1,5 | 4 | 16 | 8,25 |
| Фёдорова | 17 | 83 | 7 | 1,5 | 5,5 | 30,25 | 10,5 |
| Богданов | 19 | 54 | 3,5 | 12 | -8,5 | 72,25 | 42 |
| Суббота | 10 | 64 | 11,5 | 9 | 2,5 | 6,25 | 103,5 |
| Луц | 13 | 66 | 10 | 8 | 2 | 4 | 80 |
| Колесников | 20 | 82 | 2 | 3 | -1 | 1 | 6 |
| Мащенко | 10 | 49 | 11,5 | 13 | -1,5 | 2,25 | 149,5 |
| Коркос | 8 | 55 | 13 | 11 | 2 | 4 | 143 |
| Кладка | 16 | 69 | 8 | 7 | 1 | 1 | 56 |
| Фиткулов | 14 | 58 | 9 | 10 | -1 | 1 | 90 |
| ∑ | 164,5 | 735,5 |
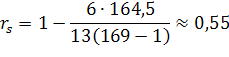
Найденное значение является приближенным, поскольку в рассмотренном примере есть так называемые связанные ранги. В этом случае лучший результат дает применение следующей формулы, которая эквивалентна предыдущей:
Вычислим по предыдущим данным ранговый коэффициент корреляции Спирмена по этой формуле. Имеем:
