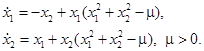Реферат: Устойчивость систем дифференциальных уравнений

2)

Задача Коши для системы (1) ставится следующим образом: найти решение  системы, определенное РІ окрестности точки , которое удовлетворяет начальным условиям  …, , где  — заданная точка РёР· области G . Решение задачи Коши существует Рё единственно, если РІСЃРµ функции РІ правых частях уравнений системы (1) непрерывно дифференцируемы РїРѕ всем В РІ окрестности точки .

Каждому решению системы (1) сопоставляется 2 геометрических объекта: интегральная кривая и траектория.

Определение . Если  — решение системы (1) РЅР° промежутке (a , b ), то множество точек (x , ), , (n +1)-мерного пространства называется интегральной кривой решения, а множество точек (), , n -мерного пространства называется траекторией решения. Заметим, что из существования и единственности решения задачи Коши интегральные кривые не могут пересекаться или иметь общих точек, однако траектории могут пересекаться без нарушения единственности, так как начальная точка определяется n +1 координатой. В частности траектория может совпадать с точкой (положение равновесия).

Система (1) называется автономной , если в правые части уравнений не входит явно независимая переменная. Система (1) называется линейной , если она имеет вид:

,

или в матричной форме В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В (1')

где В , .

Фундаментальной матрицей линейной однородной системы называется матричная функция F(t ), определитель которой отличен от нуля и столбцы которой являются решениями системы: . С помощью фундаментальной матрицы F(t ) общее решение системы можно записать в виде . Фундаментальная матрица, обладающая свойством , называется нормированной при . Если  — нормированная РїСЂРё  фундаментальная матрица, то частное решение системы записывается РІ РІРёРґРµ , где  — начальное РїСЂРё  значение решения.

1.2. Траектории автономных систем.

Будем рассматривать автономную систему в векторной форме:В В В В В В В В В В В В В В В В В В (2)
где функция f (x ) определена в .

Автономные системы обладают тем свойством, что если  — решение уравнения (2), то , , также решение уравнения (2). Отсюда в частности следует, что решение  можно записать РІ РІРёРґРµ . В геометрической интерпретации эта запись означает, что если две траектории уравнения (2) имеют общую точку, то они совпадают. При этом можно заметить, что траектория вполне определяется начальной точкой , поэтому можно везде считать .

Пусть  — положение равновесия, С‚. Рµ. . Для того чтобы точка  была положением равновесия, необходимо Рё достаточно, чтобы . Предположим теперь, что траектория решения В РЅРµ является положением равновесия, РЅРѕ имеет кратную точку, С‚. Рµ. существуют , такие, что . Так как  — РЅРµ положение равновесия, то . Поэтому можно считать, что В РїСЂРё . Обозначим В Рё покажем, что  — w-периодическая функция.

Действительно, функция  является решением уравнения (2) РїСЂРё , причем . В силу единственности В Рё  совпадают РїСЂРё всех . Применяя аналогичное рассуждение к решению , получим, что  определено РїСЂРё В Рё функции В Рё  совпадают РїСЂРё этих t . Таким образом, можно продолжить В РЅР° РІСЃРµ , при этом должно выполняться тождество

,

то есть  — периодическая функция СЃ наименьшим периодом.

Траектория такого решения является замкнутой кривой. Из приведенного вытекает следующий результат: Каждая траектория автономного уравнения (2) принадлежит одному из следующих трех типов:

1) положение равновесия;

2) замкнутая траектория, которой соответствует периодическое решение с положительным наименьшим периодом;

3) траектория без самопересечения, которой соответствует непериодическое решение.

1.3. Предельные множества траекторий.

Определение . Точка  называется w-предельной точкой траектории , , если существует последовательность  такая, что В РїСЂРё . Множество Wвсех w-предельных точек траектории называется ее w-предельным множеством. Аналогично для траектории В РїСЂРё  определяется понятие a-предельной точки как предела , а также A-предельного множества.

Определение . Траектория  называется положительно (отрицательно) устойчивой РїРѕ Лагранжу (РѕР±РѕР·РЅ. В ()), если существует компакт  такой, что В РїСЂРё всех В (), при которых

Можно показать, что предельное множество устойчивой по Лагранжу траектории не пусто, компактно и связно.

Траектория  называется устойчивой РїРѕ Пуассону, если каждая ее точка является a-предельной Рё w-предельной, С‚. Рµ. . Примером устойчивой по Пуассону траектории является состояние равновесия. Если же рассматривается траектория, отличная от неподвижной точки, то устойчивой по Пуассону она будет в том случае, если обладает свойством возвращаться в сколь угодно малую окрестность каждой своей точки бесконечное число раз. Поэтому устойчивыми по Пуассону будут циклы и квазипериодические траектории (суперпозиция двух периодических колебаний с несоизмеримыми частотами), а также более сложные траектории, возникающие в хаотических системах.

Рассмотрим (без доказательств) некоторые свойства предельных множеств в случае n = 2.

1. Предельные множества траекторий автономных систем состоят из целых траекторий.

2. Если траектория содержит по крайней мере одну свою предельную точку, то эта траектория замкнутая или представляет собой точку покоя.

3. Если траектория остается в конечной замкнутой области, не содержащей точек покоя системы, то она либо является циклом, либо спиралевидно приближается при В Рє некоторому циклу.

4. Пусть в некоторой окрестности замкнутой траектории  нет РґСЂСѓРіРёС… замкнутых траекторий. РўРѕРіРґР° РІСЃРµ траектории, начинающиеся достаточно близко РѕС‚ j, спиралевидно приближаются Рє jРїСЂРё  или РїСЂРё .

Пример . Рассмотрим автономную систему РїСЂРё :