Реферат: Узагальнена функція Гріна

Найзручнішим буде такий вибір:

Легко перевірити, що ця функція не лише задовольняє умови (10), а й є розв’язком неоднорідного рівняння = . При цьому, якщо додатково вимагати, аби розв'язок був ортогональним до на ,то .

Тепер залишилось покласти

І вибрати функцію так, щоб була ортогональною до . Для цього домножимо праву частину останньої нерівності на , одержаний добуток зінтегруємо за змінною і результат прирівняємо до нуля. З одержаного рівняння легко знайдемо

.

Остаточно маємо

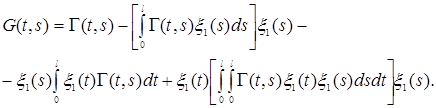(11)

З урахуванням властивостей цієї функції дамо таке означення.

Означення.

Функцію називатимемо узагальненою функцією Гріна крайової задачі (2)-(3), якщо вона задовольняє такі умови:

1. Функція неперервна в квадраті К =,має неперервні частинні похідні , у кожному з трикутників ,;

2. Для кожного фіксованого функція задовольняє рівняння Lx ( t )= -при всіх ,, а також крайовій умові (2).

3. На діагоналі квадрата К похідна має розрив першого роду зі стрибком 1/p(s): -.

4. Для кожного фіксованого функція ортогональна до функції : .

5.

Сформулюємо алгоритм відшукання узагальненої функції Гріна.

· Знаходимо таку фундаментальну систему , лінійного однорідного рівняння (1), щоб розв'язокзадовольняв умови(2).

· Знаходимо будь-який розв'язокg ( t , s ) неоднорідного рівняння Lx ( t )= -.

· Узагальнену функцію Гріна шукаємо у вигляді

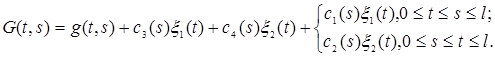
Функції обираємо так, щоб останній доданок задовольняв пунктам 1 і 3 означення узагальненої функції Гріна;функцію - так, щоб задовольняла крайові умови задачі;нарешті, вибором функції забезпечуємо виконання умови ортогональності 4.

Проаналізувавши вигляд правої частини формули (11), можна зробити висновок, що з потрібними властивостями існують.

Розглянемо приклад.

Розв’яжемо крайову задачу

, << ;

Розв'яжемо відповідне однорідне рівняння , застосувавши метод Ейлера. Тобто розв'язок шукаємо у вигляді= . Знайшовши