Реферат: Узагальнена функція Гріна

З цього маємо фундаментальну систему розв’язків рівняння:

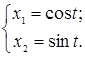
За теоремою про загальний розв'язокоднорідного рівняння, маємо:

де

Тому можемо сказати, що відповідна однорідна задача має однопараметричну сім’ю розв’язків , де – довільна стала, для якої умова теореми 1 виконано, бо 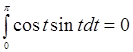. Методом невизначених коефіцієнтів знайдемо частинний розв’язок диференціального рівняння задачі: . Загальний розв’язок цього рівняння має вигляд:

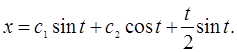
Для того, щоб задовольнити крайовій умові, достатньо покласти . Сталу виберемо так, щоб справджувалась умова ортогональності шуканого розв’язку й функції :

Звідси =. Остаточно маємо:

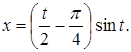
Знайдемо функцію Гріна для цієї крайової задачі

За функцію візьмемо 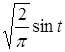(коефіцієнт вибирається з умови нормованості ) Розв'язком однорідного рівняння, який не задовольняє крайові умови, є, наприклад .

Далі рівняння

Має частинний розв'язок вигляду , отже, узагальнену функцію Гріна шукаємо у вигляді

(коефіцієнт вбирають у себе функції і ).

Оскільки в нашому випадку, то умови неперервності і стрибка похідної функції при мають вигляд

,.

Звідси ,;

Наслідком крайової умови в точці є рівність . Тоді в точці маємо: .Отже, функція

задовольняє пунктам 1-3 означення узагальненої функції Гріна.

Нарешті, функцію визначимо з умови ортогональності

. Обчисливши відповідні інтеграли, знаходимо

Остаточно маємо