Реферат: Вероятности, энтропия и энергия. Канонический ансамбль Гиббса

Набором квантовых состояний – уровней определяется любого коллектива целиком определяется его полная статистическая сумма состояний и его свободная энергия

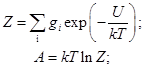(4.1)

Канонический ансамбль состояний описывает реальную изотермическую систему при постоянной температуре. Коллектив - система может быть макроскопическим, и должен состоять из огромного числа однотипных подсистем.

Если коллектив состоит из микроскопических элементов –атомов и молекул, то в отсутствие взаимодействий между ними получаем модель статистического идеального газа.

Каноническое распределение Гиббса становится распределением Больцмана, а факторы Гиббса превращаются в факторы Больцмана. Статистические свойства идеального газа блестяще описываются даже на основе простейших квантовых моделей молекулярных движений с поправками, посредством которых учитываются свойства симметрии коллектива.

5. Идеальный газ. Распределение Больцмана.

Распределение Больцмана описывает изотермическую систему множества однотипных невзаимодействующих между собою частиц. Поэтому его называют распределением для идеального газа. Это предел распределения Гиббса для коллектива и ансамбля состояний частиц идеального газа.

Для такого случая символ Z полной статистической суммы коллектива заменяется символом Q полной статистической суммы идеального газа.

6. Уровни простейших стационарных движений.

Уровни квантовых систем получают из уравнения Шрёдингера.

6.1) Простейшее поступательное движение. Уровни одномерного ящика.

Поступательные уровни замкнутой системы – «ящика».

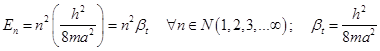; (6.1)

6.2) Простейшее вращательное движение. Ротатор.

Вращательные уровни линейной частицы

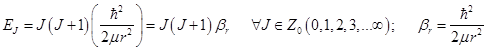; (16.2)

; (16.3)

16.3) Простейшее колебательное движение. Осциллятор (Вибратор).

Колебательные уровни.

; (6.4)

7. Статистические суммы для простейших стационарных движений.

7.1) Поступательная статистическая сумма одномерного движения.

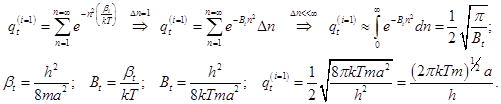(7.1)

Здесь использован стандартный интеграл – интеграл Пуассона ; (17.2)

ВНИМАНИЕ! Результат предварительный: ; (7.3)

Полученное выражение необходимо скорректировать и учесть неразличимость частиц вследствие перемешивания газа за счёт броуновского движения.

7.2) Вращательная статистическая сумма линейной молекулы.

Расчёт приближённый – для молекул с достаточно большой массой обоих атомов.

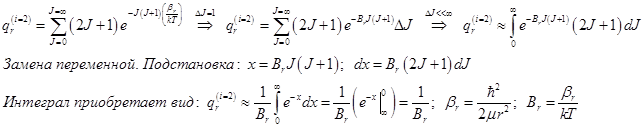(17.4)