Реферат: Вероятности, энтропия и энергия. Канонический ансамбль Гиббса

Формула применима для частиц с очень близко расположенными вращательными уровнями. Это имеет место у молекул тяжёлых. Для молекул, содержащих водород и его изотопы эта формула не вполне точна, и статистическая сумма вращения вычисляется численно прямым суммированием.

ВНИМАНИЕ! Результат предварительный: ; (7.5)

Полученное выражение необходимо скорректировать и учесть неразличимость ориентаций молекулы, возникающих при её самосовмещении при повороте.

7.3) Статистическая сумма для гармонического колебания.

Расчёт проводится от нуля энергии колебания. Квантовое число основного уровня v=1/2 отвечает низшему колебательному уровню

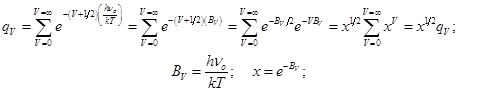; (7.6)

Если то сумма представляет собой убывающую геометрическую прогрессию. Это даёт возможность выполнить простые преобразования:

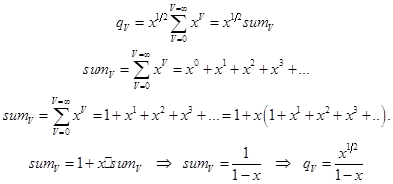; (7.7)

Получено выражение колебательной суммы состояний при отсчёте энергии от запрещённого для осиллятора нулевого значения.

Результат: 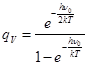; (7.8)

18.2) Вибрационная сумма состояний (от E=0) (1 степень свободы).

Формулу (18.1) можно представить равносильным способом.

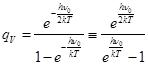; (8.1)

8.3) Вибрационная сумма состояний (от основного уровня V=1/2, E=hn0/2).

При отсчёте энергии уровней от минимально допустимого значения (от уровня с колебательным квантовым числом V=1/2) статистическая сумма (7.8 или 8.1) упрощается, принимая вид (8.2). Это удобнее для практических вычислений, поскольку энергия колебаний отсчитывается уже непосредственно от уровня основного электронно-колебательного состояния - D, от которого определяется энергия диссоциации молекулы или соответствующей химической связи на нейтральные атомы. Такая диссоциация требует меньших затрат, но возможен распад связи и на заряженные ионы. Для этого необходимы дополнительные затраты энергии на преодолению сил кулоновского притяжения ионов, а энергия диссоциации на ионы возрастает.

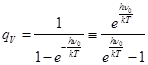; (8.2)