Реферат: Вероятности, энтропия и энергия. Канонический ансамбль Гиббса

Микросостояния в ансамбле для удобства пронумеруем множеством {…, a, a+1,…i,…}. Построить необходимые математические соотношения, описывающие свойства канонического ансамбля Гиббса, можно проще всего, исходя из хорошо известных формул классической феноменологической термодинамики.

КАНОНИЧЕСКИЙ АНСАМБЛЬ образован из состояний равновесной изохорно-изотермической системы (V,T=const).

Каждое микросостояние совместимо с наблюдаемым макросостоянием коллектива, и это означает, что все они характеризуются одним и тем же значением наблюдаемых макроскопических параметров и свободной энергии A, т.е.:

; (1)

В разных микросостояниях энтропия и внутренняя энергия (Ui; Si) системы могут различаться, но неизменна их свободная энергия. Справедлива цепочка равенств:

; (2)

Энтропия S статистического коллектива и термодинамическая вероятность W связаны законом Больцмана-Планка: ; (3)

Отсюда возникает цепочка равенств:

(4)

Термодинамическая вероятность W макросостояния коллектива это число всех приводящих к нему комбинаций всех элементов между их возможными микросостояниями.

Каждая из комбинаций и порождает отдельное микросостояние колектива.

Поэтому всегда W>1. Очевидно минимум W =1 имеет место лишь в предельном случае идеально упорядоченного состояния коллектива (на атомно-молекулярном уровне – это состояния идеального кристалла), а во всех прочих случаях она больше единицы W>1.

Важны некоторые простые и почти очевидные соображения.

1. Вероятности и статистические суммы.

Математическая вероятность w каждого из микросостояний, входящих в макросостояние, это его доля во всём ансамбле, т.е. доля в макросостоянии. Она обратна термодинамической вероятности w =1/W и меньше единицы w <1.

Математические вероятности можно нормировать:

(1.1)

Всем микросостояниям отвечает одинаковая свободная энергия A, и поэтому множитель с нею можно вынести за знак суммы:

(1.2)

Второй сомножитель содержит сумму всех факторов Гиббса. Его называют суммой состояний, или суммой по состояниям, или статистической суммой исследуемого статистического коллектива (термодинамической системы) и обозначают как

(1.3)

Получаются очевидные соотношения,

; (1.4)

Вероятность микросостояния это одно из слагаемых суммы, и его можно выделить ; (1.5)

Часто применяется форма канонического распределения:

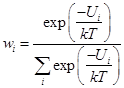; (1.6)

2. Каноническое распределение по состояниям.

Запишем основную формулу:

(2.1)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--