Реферат: Виды рядов распределения

Мода - это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.

В интервальном ряду распределения мода находится по следующей формуле:

(4) ,

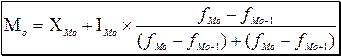где: минимальная граница модального интервала;

- величина модального интервала;

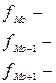{частоты модального интервала, предшествующего и следующего за ним

Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.д.

Медиана - варианта, находящаяся в середине ряда распределения.

Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы.

В случае если вариационный ряд имеет число значений вариант четное, то расчет медианы производится по следующей формуле:

(5) 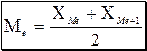, где - варианты, находящиеся в середине ряда

В интервальном ряду распределения медиана рассчитывается следующим образом:

(6) ,

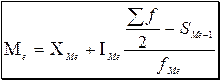где: - нижняя граница медианного интервала;

- величина медианного интервала;

- полусумма частот ряда;

- сумма накопленных частот, предшествующих медианному интервалу;

- частота медианного интервала.

Структурные средние величины (мода и медиана) имеют довольно большое значение в статистике и широкое применение. Мода является именно тем числом, которое в действительности встречается наиболее часто. Медиана имеет важные свойства для анализа явлений: она обнаруживает типичные черты индивидуальных признаков явления, и, вместе с тем, учитывает влияние крайних значений совокупности. Медиана находит практическое применение в маркетинговой деятельности вследствие особого свойства – сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая:

Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного расположения частот вариационного ряда.

1.5. Графическое изображение статистических данных

Ряды распределения удобно изучать с помощью графического метода.

Статистический график– это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков. Представление данных таблиц в виде графика производит более сильное впечатление, чем цифры, позволяет лучше осмыслить результаты статистического наблюдения, правильно их истолковывать, значительно облегчает понимание статистического материала, делает его наглядным и доступным. Это, однако, вовсе не означает, что графики имеют лишь иллюстративное значение. Они дают новое знание о предмете исследования, являясь методом обобщения исходной информации.

Значение графического метода в анализе и обобщении данных велико. Графическое изображение позволяет осуществить контроль достоверности статистических показателей, так как, представленные на графике, они более ярко показывают имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления. С помощью графического изображения возможны изучение закономерностей развития явления, установление существующих взаимосвязей. Простое сопоставление данных не всегда дает возможность уловить наличие причинных зависимостей, в то же время их графическое изображение способствует выявлению причинных связей, в особенности в случае установления первоначальных гипотез, подлежащих затем дальнейшей разработке. Графики также широко используются для изучения структуры явлений, их изменения во времени и размещения в пространстве. В них более выразительно проявляются сравнительные характеристики и отчетливо виды основные тенденции развития и взаимосвязи, присущие изучаемому явлению или процессу.

Таблица 2.

1995	1996	1997	1998	1999	2000
Валовой внутренний продукт в рыночных ценах	1 428,5	2 007,8	2 342,5	2 629,6	4 823,2	7 305,6

*Номинальный объем произведенного ВВПв текущих ценах, млрд.рублей, до 1998г. - трлн.рублей[1]

Рис.1. График динамики произведенного объема ВВП.

Для изображения и внесения суждений о развитии явления во времени и составе совокупности наряду с графиками строятся диаграммы.

Используются диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, радикальные и др. Выбор вида диаграммы зависит в основном от особенностей исходных данных, цели исследования. Например, если имеется ряд динамики с несколькими неравноотносящимися уровнями во времени (1913, 1940, 1950, 1980, 1985, 1997 гг.), то часто для наглядности используют столбиковые, квадратные или круговые диаграммы. Они зрительно впечатляют, хорошо запоминаются, но не годны для изображения большого числа уровней, так как громоздки. Когда число уровней в ряду динамики велико, целесообразно применять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломанной линии. Кроме того, линейные диаграммы удобно использовать: если целью исследования является изображение общей тенденции и характера развития явления; когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения; если наиболее существенным является сопоставление темпов роста, а не уровней.