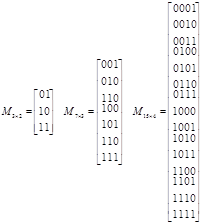011001

111111

Перший рядок в ній - це рядок кодових слів, а перший стовпець - це лідери.

Щоб декодувати слово b_j +e, слід відшукати його в таблиці і вибрати як переданого слово в тому ж стовпці і в першому рядку.

Наприклад, якщо прийнято слово 110011 (2-й рядок, 3-й стовпець таблиці), то вважається, що було передане слово 010011; аналогічно, якщо прийнято слово 100101 (3-й рядок, 4-й стовпець таблиці), за передане вважається слово 110101, і так далі

Групове кодування з схемою декодування за допомогою лідерів виправляє всі помилки, рядки яких збігаються з лідерами. Отже, вірогідність правильного декодування переданої по двійковому симетричному каналу коди дорівнює сумі вірогідності всіх лідерів, включаючи нульовий.

У розглянутій схемі вірогідність правильної передачі слова буде

p⁶ +6p⁵ q+p⁴ q² .

Кодове слово будь-якого стовпця таблиці декодування є найближчим кодовим словом до всіх інших слів даного стовпця.

Хай передане слово b_i прийняте як b_i +e, d(b_i ,b_i +e)=u(e), тобто ця відстань дорівнює вазі відповідного лідера. Відстань від b_i +e до будь-якого іншого кодового слова b_j дорівнює вазі їх порозрядної суми, тобто

оскільки e- лідер суміжного класу, до якого належать як b_k +e, так і b_i +e.

Доведено, при схемі декодування лідерами по отриманому слову береться найближче до нього кодове.

Досконалі і квазідосконалі коди

Груповий -код, що виправляє всі помилки ваги, не більшої k, і ніяких інших, називається досконалим.

Властивості досконалого коду:

1. Для досконалого -кода, що виправляє всі помилки ваги, не більшої k, виконується співвідношення . Вірно і зворотне твердження;

2. Досконалий код, що виправляє всі помилки ваги, не більшої k, в стовпцях таблиці декодування містить всі слова, віддалені від кодових на відстані, не більшому k. Вірно і зворотне твердження;

3. Таблиця декодування досконалого коду, що виправляє всі помилки в не більше ніж k позиціях, має як лідерів всі рядки, що містять не більш k одиниць. Вірно і зворотне твердження.

Досконалий код - це кращий код, що забезпечує максимум мінімальної відстані між кодовими словами при мінімумі довжини кодових слів. Досконалий код легко декодувати: кожному отриманому слову однозначно ставиться у відповідність найближчу кодову. Чисел m, n і , що задовольняють умові досконалості коди, дуже мало. Але і при підібраних m, n і k досконалий код можна побудувати тільки у виняткових випадках.

Якщо m, n і k не задовольняють умові досконалості, то кращий груповий код, який їм відповідає, називається квазідосконалим, якщо він виправляє всі помилки кратності, не більшої k, і деякі помилки кратності k+1. Квазідосконалі код також дуже мало.

Двійковий блоковий -код називається оптимальним, якщо він мінімізує вірогідність помилкового декодування. Досконалий або квазідосконалий код - оптимальний. Загальний спосіб побудови оптимальних код поки невідомий.

Для будь-якого цілого позитивного числа r існує досконалий -код, що виправляє одну помилку, званий кодом Хеммінга (Hamming), в якому і .

Дійсно

.

Порядок побудови коди Хеммінга наступний:

1. Вибираємо ціле позитивне число r. Повідомлення будуть словами довжини , а кодові слова - довжини ;

2. У кожному кодовому слові r біт з індексами-ступенями двійки - є контрольними, останні - в природному порядку - бітами повідомлення. Наприклад, якщо r=4, то биті - контрольні, а - з початкового повідомлення;

3. Будується матриця M з рядків і r стовпців. У i-ому рядку стоять цифри двійкового представлення числа i. Матриці для r=2, 3 і 4 такі: