Реферат: Волновые процессы и элементы векторного анализа
![]()
![]() ;
; 
В фиксированный момент времени;
![]() ,
, ![]() ,
, 
2.4. Фазовая скорость
Фазовая скорость и волны есть скорость распространения точек одинаковой фазы:
![]()
Эта скорость равна скорости гармонической волны. Фазовая скорость:
u=![]() /k=
/k=![]()
![]()
k=2![]() т.е.u=
т.е.u=![]()
|
|
![]() t-kx-
t-kx-![]() =const дифференцируем
=const дифференцируем
|
|
![]()
![]()
![]()
![]()
|
|
|
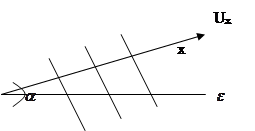
UЕ =Ux /cos![]() т.е. т.к. cos
т.е. т.к. cos![]() <1,.
<1,.
то фазовая скорость может превышать скорости света
Элементы векторного анализа
Необходимо уметь анализировать не только скалярные, но и векторные функции точки.Скалярные функции: температура неравномерно нагретого тела, плотность неоднородного тела и т. д.Векторные функции: скорость частиц текущей жидкости, сила земного притяжения, магнитное и электрическое напряжение электрического поля.Рассмотрение скалярных и векторных функций точки привело к построению теории поля.
Векторное поле а(М) называется дифференцируемым в точке М, если оно определено в окрестности точки М и если приращение ∆a=a(M’)-a(M) поля может быть представлено в виде:
∆a=А(∆r)+E(∆r);
∆r=MM ’ ; A и E – линейные операторы;
А – не зависит от ∆r; E зависит, при ∆r=0 E=0;
Необходимое и достаточное условие дифференцируемости векторного поля а заключается в дифференцируемости его координат P, Q, R. При этом линейный оператор А изображается матрицей:
![]()
![]() дР/дх, дР/ду, дР/д z
дР/дх, дР/ду, дР/д z
А= д Q /дх, д Q /ду, д Q /д z
д R /дх, д R /ду, д R /д z
и вектор-функция А(∆r) имеет вид:
A(∆r)=1/2{A(∆r)+A* (∆r)}+1/2[p A(r)].
Дивергенция
Сумма диагональных элементов матрицы, представляющей симметричную линейную вектор-функцию ½{A(∆r)+A* (∆r)} не зависит от выбора системы координат: она называется дивергенцией (расхождением) векторного поля а и обозначается diva :
diva =д P /дх+д Q /ду+д R /д z .
Вектор Р называется вихрем (ротором) поля а и записывается в виде:
rota =(д R /ду-д Q /д z ,дР/д z - R д/дх, д Q /дх-дР/ду );
Если V поле скоростей текущей жидкости и rotV ≠ 0, то частица движется по замкнутым линиям (образуются вихри). divV в этом случае характеризует интенсивность источника divV >0 и стока divV <0, находящегося в этой точке или отсутствие источника и стока.
Сегодня общепринято представлять уравнения Максвелла в векторной форме. Описания в декартовых координатах менее информативно.
Мы в основном будем пользоваться следующимиобозначениями:
1.Всегда используется правая системакоординат: т.е. такая вкоторой положительная ось Х совмещается с осью У,если наблюдатель смотрит вдоль положительного направления оси Z.
2.Векторы обозначаются буквами: