Реферат: Волны в упругой среде. Волновое уравнение

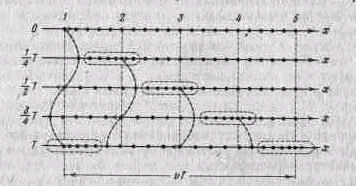
На рис. 2 показано движение частиц при распространении в среде продольной волны. Все рассуждения, касающиеся поведе­ния частиц в поперечной волне, могут быть отнесены и к данному случаю с заменой смещений вверх и вниз смещениями вправо и влево. Из рисунка видно, что при распространении продольной волны в среде создаются чередующиеся сгущения и разрежения частиц (места сгущения частиц обведены на рисунке пунктиром), перемещающиеся в направлении распространения волны со ско­ростью v.

Рисунок 2

§ 2. Фронт волны. Длина волны.

На рис. 1 и 2 показаны колебания частиц, положения равновесия которых лежат на оси х. В действительности колеблют­ся не только частицы, расположенные вдоль оси х, а совокупность частиц, заключенных в некотором объеме. Распространяясь от ис­точника колебаний, волновой процесс охватывает все новые и но­вые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом ). Фронт волны пред­ставляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой ко­лебания еще не возникли.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью . Волновую по­верхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается.

Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сфериче­ской. В плоской волне волновые поверхности представляют со­бой множество параллельных друг другу плоскостей, в сфериче­ской волне — множество концентрических сфер.

Рассмотрим случай, когда плоская волна распространяется вдоль оси х. Тогда все точки среды, положения равновесия кото­рых имеют одинаковую координату х (но различные значения координат y и z), колеблются в одинаковой фазе.

Рисунок 3

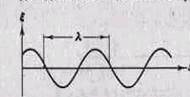
На рис. 3 изображена кривая, которая дает смещение из положения равновесия точек с различными x в некоторый мо­мент времени. Не следует воспринимать этот рисунок как зримое изображение волны. На рисунке показан график функции (х, t) для некоторого фиксированного момента времени t. С течением времени график перемещается вдоль оси х. Такой график можно строить как для продольной, так и для поперечной волны. В обоих случаях он выглядит одинаково.

Расстояние , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны . Очевидно, что

=vТ, (1.1)

где v – скорость волны, Т – период колебаний. Длину волны можно определить также как расстояние между ближайшими точками среды, колеблющимися с разностью фаз, равной 2П. Заменив в соотношении (1.1) Т через 1/ ( – частота колебаний), получим

=v (1.2)

Рассмотрев кратко основные понятия, связанные с волной, перейдем к описательной стороне, т.е. волновому уравнению.

Глава II.

Волновое уравнение.

§ 1. Математические сведения.

Этот параграф является математическим введением к тому динами­ческому рассмотрению волн, которое будет дано в $2. Рассмотрим произвольную функцию

f(at-bx) (2.3) от аргумента а t— bх. Продифференцируем ее дважды по t:

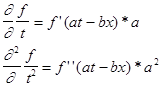(2.4)

Здесь штрих означает дифференцирование по аргументу at—bx. Продифференцируем теперь нашу функцию дважды по х:

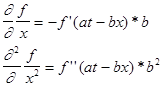(2.5)

Сравнивая (2.4) и (2.5), мы убеждаемся, что функция (2.3) удовлетво­ряет уравнению

(2.6)

где

u=a/b.

Легко видеть, что этому же уравнению удовлетворяет произвольная функция

f(at+bx) (2.7) (2.7) аргумента at+bx, а также сумма функций вида (2.3) и (2.7).

Функции (2.3) и (2.7) изображают при положительных a, b пло­ские волны, распространяющиеся, не деформируясь, со скоростью и в сто­рону соответственно возрастающих или убывающих значений х **).

Уравнение (2.6)—дифференциальное уравнение в частных производ­ных, играющее в физике очень важную роль. Оно называется волновым уравнением. В математических курсах доказывается, что оно не имеет решений, отличных от тех, которые могут быть представлены функциями вида (2.3) и (2.7) или суперпозицией таких функций, например,