Реферат: Введение в теорию атома

8.5. Перевод лапласиана в шаровые координаты можно осуществить, следуя различным схемам. В сферических координатах лапласиан выглядит на первый взгляд довольно внушительно, но при ближайшем рассмотрении оказывается конструкцией, достаточно простой. Несложные, но довольно длительные преобразования приводят к следующему выражению:

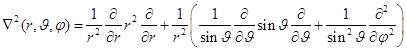. (8.3)

8.6. Компоненты лапласиана.

Для сокращения выделим в лапласиане два слагаемых - радиальное и угловое:

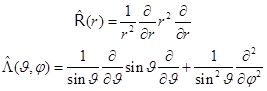(8.4)

Угловой оператор называется оператором Лежандра.

Лапласиан приобретает сжатый вид:

(8.5)

8.7. Угловой оператор(оператор Лежандра)

в свою очередь разделяется далее на два независимых оператора. Один действует на переменную долготы J, второй - на переменную широты j, и получается:

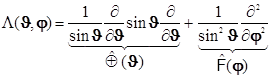
. (8.6)

Операторное уравнение для оператора Лежандра встречается в нескольких очень важных фундаментальных ситуациях. Это задачи: 1) о квантовых состояниях и энергетических уровнях ротатора - линейной молекулы, свободно вращающейся вокруг центра массы. 2) об электронном строении атома H и водородоподобных ионов.

8.8. Уравнение Лапласа для сферической системы:

Уравнением Лапласа называется дифференциальное уравнение в частных производных второго порядка вида 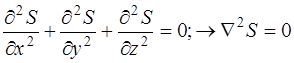. В сферических переменных оно имеет вид

. (8.7)

. (8.8)

Решения находятся по методу Фурье: для разделения переменных искомое решение представляется в виде произведения радиальной и угловой компонент функций.

8.9. Разделение переменных.

Общее правило: Если в дифференциальном уравнении в частных производных можно выделить оператор, включающий несколько переменных, и привести его к аддитивной форме, придавая ему вид суммы слагаемых, определённых лишь для отдельных переменных, то исходное дифференциальное уравнение распадается на систему дифференциальных уравнений.

Каждое из них и их решения определены лишь на переменных соответствующего оператора-слагаемого. Частные решения исходного дифференциального уравнения выбираются в мультипликативном виде, как произведения функций – решений отдельных уравнений системы. Этот результат сформулируем в виде краткого правила: «Оператор аддитивен-Решения мультипликативны». Этот подход встречается всюду в теории многоэлектронных систем – атомов и молекул.

8.10. Радиальная часть общего решения сферического уравнения Лапласа выбрана в виде степенной функции от радиальной переменной с показателем степени l принимающим одно из целочисленных неотрицательных значений. В этом случае соблюдается симметрия общего решения по отношению к взаимным перестановкам декартовых координат, и делается возможно построение регулярных решений (функций класса Q ), которые обладают известными свойствами конечности, однозначности и непрерывности, а также могут быть и пронормированы.

. (8.9)

Угловые сомножители общего решения Y (J,j) называются сферическими гармониками (шаровыми функциями). Запишем уравнение Лапласа, и рассмотрим процедуру разделения переменных:

. (8.10)

Учитывая, что каждый из операторов активен лишь к своим переменным, получаем:

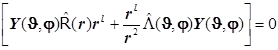. (8.11)

Для разделения переменных следует слева умножить каждое из слагаемых в уравнении на функцию, обратную искомому общему решению. Эта функция равна :

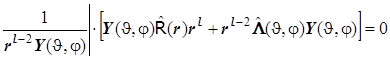
8.11. Получаем равенство, обе части которого содержат независимые переменные и поэтому их обе следует приравнять постоянной величине, т.е.: