Реферат: Выборочное наблюдение

t

0,683

1,0

0,954

2,0

0,997

3,0

Примечание : при t=1,0, предельная ошибка выборки обращается в среднюю ошибку выборки . .

Разные способы организации выборочного наблюдения обеспечивают случайность отбора с разной степенью репрезентативности, что отражается на особенностях расчета ошибок выборки.

Основные способы отбора:

1. Собственно-случайный отбор (лотерея, жеребьевка, отбор на основе таблицы случайных чисел). Он может быть как повторным, так и бесповторным. Поэтому для расчета ошибки выборки используются формулы (1) и (2).

2. Механический отбор – это когда упорядоченно расположенные единицы совокупности отбирают по одной через определенный интервал, называемый шагом выборки. Шаг выборки – величина обратная относительному объему выборки; например, при 10% - ной выборке равен 10 (100:10), при 4%-ной – 25 (100:4) и т.д.

Механический отбор всегда бесповторен, поэтому для расчета ошибки выборки используется только формула (2).

3. Типическая выборка обеспечивает наибольшую репрезентативность, но при этом требует особой организации своего проведения.

Вначале генеральная совокупность разбивается на качественно однородные группы (объединяющие единицы совокупности по типам явлений), затем из каждой выделенной группы (выделенного типа явлений) в случайном порядке отираются отдельные единицы, как правило, в объеме, пропорциональном численности единиц по группам в генеральной совокупности.

Формула расчета ошибки типического отбора

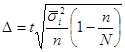, (3)

где - средняя из внутригрупповых дисперсий.

4. Серийная (гнездовая) выборка обеспечивает наименьшую репрезентативность, но при этом является самым легким, быстрым, наименее трудоемким, дешевым способом организации отбора. Здесь из генеральной совокупности отбирают не отдельные единицы, а целые их группы (серии, гнезда). Внутри отобранной серии производят сплошное наблюдение.

Ошибка выборки принимает вид:

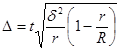, (4)

– число серий (гнезда) в генеральной совокупности;

– число серий в выборочной совокупности;

– межгрупповая (межсерийная) дисперсия признака.

3 Распространение выборочных данных на генеральную совокупность

Выборочное наблюдение проводится в целях распространения выводов, полученных по данным выборки, на генеральную совокупность.

Пределы, в которых находятся значения характеристик в генеральной совокупности при заданном уровне вероятности, следующие:

- для средней; (5)

- для доли. (6)

Это означает, что с заданной вероятностью можно утверждать, что значение генеральной характеристики следует ожидать в этих пределах.

Покажем на примерах как определять пределы.