Реферат: Задача Лагранжа

Примем следующие обозначения:

q - объем заказа (при пополнении запасов);

q0 - оптимальный размер заказа;

t - интервал времени;

ts - интервал времени между двумя заказами;

tso - оптимальный интервал времени между заказами;

T - период времени, для которого ищется оптимальная стратегия;

R - полный спрос за время Т;

C1 - стоимость хранения единицы продукции в единицу времени;

C2 - величина штрафа за нехватку одной единицы продукции (в определенный момент времени).

Cs- стоимость заказа ( при покупке или производстве),

Cs - ожидаемые суммарные накладные расходы;

Qo- минимум ожидаемых суммарных накладных расходов;

So - оптимальный уровень запасов к началу некоторого интервала времени.

Модель I .

Пусть некий предприниматель должен поставлять своим клиентов R изделий равномерно в течение интервала времени Т. таким образом, спрос фиксирован и известен. Нехватка товара не допускается, т.е. штраф при неудовлетворенном спросе бесконечно велик (C2=µ). Переменные затраты производства складываются из следующих элементов: C1 - стоимость хранения одного изделия (в единицу времени), C2- стоимость запуска в производство одной партии изделий.

Предприниматель должен решать, как часто ему следует организовывать выпуск партии и каким должен быть размер каждой партии.

Уравнение цен и его аналитическое решение. Только чтоописанная ситуация представлена графически на рис.5. Пусть q -размер партии, ts - интервал времени между запусками в производство партии, а R - полный спрос за всё времени планирования T.

????? R/q ? ????? ?????? ?? ????? ? ?

Если интервал ts начинается, когда на кладе имеется q изделий и заканчивается при.

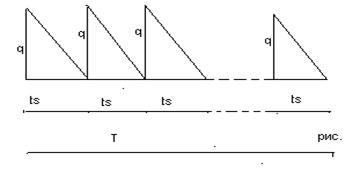
отсутствии заказов, тогда q/2 – средний запас в течение ts(равенство q/2= qсрследует рассматривать как приближенное. Точность его тем выше, чем больше R) q/2* C1tsзатраты на хранения в интервале ts.

Общая стоимость создания запасов в интервале ts равна сумме стоимости запуска в производство

??? ?????????? ?????? ????????? ???????? ??????? ?? ????? ? ??????? ??? ???????? ???????? ?? ????? ????? ?????? ?? ??? ?????:
?????????? ???? ????????? ??? ts, ????????
???

Члены в правой части уравнений (44) представляют стоимость хранения и полную стоимость заказа в производстве всех партий. С увеличением размера партий первый член возрастает, а второй убывает. Решение задачи управления запасами и состоит в определении такого размера партии qo, при котором суммарная стоимость была бы наименьшей (рис. 6)

Найденное оптимальное значение qoразмер партии

??? ??????????? ts? ? Qo?????

Пример I : Пусть предприниматель должен поставлять своему заказчику 24000 единиц продукции в год. Так как получаемая продукция используется непосредственнона сборочной линии и заказчик не имеет для нее специальных складов, поставщик должен единично отгружать дневную норму. В случаи нарушения поставок поставщик рискует потерять заказ. Поэтому нехватка продукции недопустима, т.е. штраф при нехватке можно бесконечным. Хранение единицы продукции в месяц стоит 0,1 долл. Стоимость запуска в производство одной партии продукции составляет 350 долл.

Требуется определить оптимальный размер партии q0, оптимальный период и tsовычислить минимум общих ожидаемых годовых затрат Qо. В данном случае Т = 12 месяцам, R = 24 000 единиц, Сs = 0,1 долл./партия Сs= 350 дол/партия. Подстановка этих значений в уравнения (9), (10) и (11) дает нам.

Модель II .

Рассмотрим теперь случай, который отличается от предыдущего только тем, что превышение спроса над запасами уже допускается, т.е. штраф за нехватку конечный.

Уравнение цен и его аналитическое решение. Рассматриваемая ситуация изображена на рис. 7. В начале каждого интервала имеется уровень запасов. Из подобия треугольников находим.

Средний запас в течении t1, равен S/2. Поэтому затраты на хранение за всё время t1