Реферат: Задача по Экономико-математическое моделирование

Нефтеперерабатывающий завод производит в месяц 1500000 л алкилата, 1200000 л крекинг - бензина и 1300000 л изопентола. В результате смешения этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и Б соответственно. Стоимость 1000 л бензина сорта А и Б соответственно равна 90 и 120 усл. ед.. Определить месячный план производства бензина сорта А и Б, приносящий предприятию максимальную прибыль.

Решите задачу графическим и симплекс-методом. Выполните постановку и найдите решение двойственной задачи.

1. Графический метод решения

Характеристика	Бензин		Ограничения
	А	Б
Алкилат	1	3	1500
Крекинг – бензина	1	1	1200
Изопентол	1	2	1300
Прибыль (за 1000л)	90	120
План	х1	х2

х₁ + 3х₂ < 1500,

х₁ + х₂ < 1200,

х₁ + 2х₂ < 1300,

х₁ > 0, х₂ > 0.

Целевая функция:

f = 90х₁ + 120х₂ → max.

Строим прямые

х₁ + 3х₂ = 1500, 1

х₁ + х₂ = 1200, 2

х₁ +2 х₂ = 1300. 3

Строим направляющий вектор q {90, 120}.

Строим прямую, перпендикулярную направляющему вектору и проходящую через область допустимых решений.

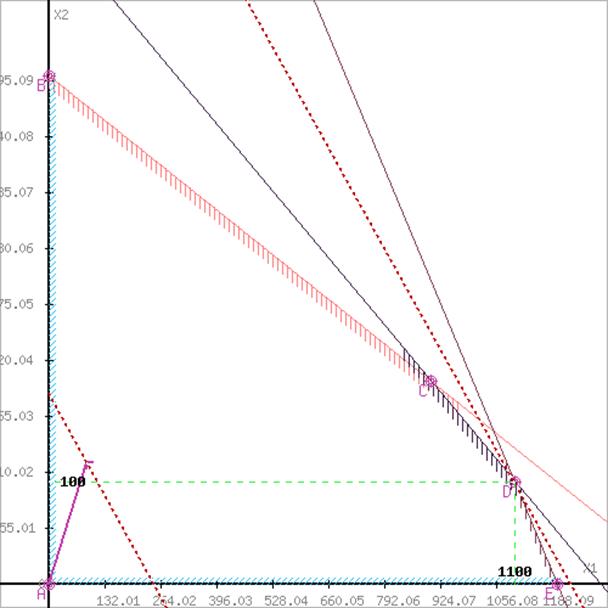
Находим оптимальный план:

х₁ + х₂ = 1200, х₁ = 1100,

х₁ +2 х₂ = 1300. х₂ = 100.

Максимальная прибыль допускается при выпуске 1100 бензина А и 100 бензина Б.

Оптимальное значение целевой функции:

f = 90х₁ + 120х₂ , f = 90∙1100 + 120∙100 = 111000.

2. Симплекс-метод.

Характеристика	Бензин		Ограничения
	А	Б
--> ЧИТАТЬ ПОЛНОСТЬЮ <-- « 1 2 3 » К-во Просмотров: 295 Бесплатно скачать Реферат: Задача по Экономико-математическое моделирование >>> Скачать <<< Меню Поиск