Реферат: Задача потребительского выбора.Функция потребительского предпочтения Стоуна

Иначе говоря, u ( x ₁ , x ₂ )= u >0 , u ( x ₁ , x ₂ )= u >0.

Первые частные производные u и u называются предельными полезностями первого и второго продуктов соответственно.

2. Предельная полезность каждого продукта уменьшается, если объём его потребления растёт (закон убывания предельной полезности ). Из свойства второй производной следует, что u ( x ₁ , x ₂ )<0, u ( x ₁ , x ₂ )<0.

3. Предельная полезность каждого продукта увеличивается, если растёт количество другого продукта. В этом случае продукт, количество которого фиксировано, оказывается относительно дефицитным. Если блага могут замещать друг друга в потреблении, свойство не выполняется. u ( x ₁ , x ₂ )= u ₁₂ >0, u ( x ₁ , x ₂ )= u ₂₁ >0.

Линия, соединяющая потребительские наборы ( x ₁ , x ₂ ) , имеющие один и тот же уровень удовлетворения потребностей называется линией безразличия . Линия безразличия есть не что иное, как линия уровня функции полезности. Множество линий безразличия называется картой линий безразличия . Линии безразличия, соответствующие разным уровням удовлетворения потребностей не пересекаются и не касаются. Чем выше и правее расположена линия безразличия, тем большему уровню удовлетворения потребностей она соответствует. Условия 1-3 означают, что линия безразличия убывает и является выпуклой вниз.

Задача потребительского выбора заключается в выборе такого потребительского набора (х, х), который максимизирует его функцию полезности при заданном бюджетном ограничении.

Бюджетное ограничение означает, что денежные расходы на продуктыне могут превышать денежного дохода, т.е.

p ₁ x ₁ + p ₂ x ₂ ≤ Q , где

p₁ и p₂ –рыночные цены,

Q – доход потребителя, который он готов потратить на приобретение первого и второго продуктов.

Величины p ₁ , p ₂ и Q заданы.

Задача потребительского выбора имеет вид:

u ( x ₁ , x ₂ )→ max

при ограничении p ₁ x ₁ + p ₂ x ₂ ≤ Q

и при условии x ₁ ≥0, x ₂ ≥0.

Допустимое множество (т.е. множество наборов продуктов, доступных для потребителя) представляет собой треугольник, ограниченный осями координат и бюджетной прямой. На этом множестве требуется найти точку, принадлежащую кривой безразличия с максимальным уровнем полезности. Поиск этой точки можно интерпретировать графически как последовательный переход на линии всё более высокого уровня полезности до тех пор, пока эти линии ещё имеют общие точки с допустимым множеством (Рис.1).

бюджетная прямая

Линиибезразличия

X1

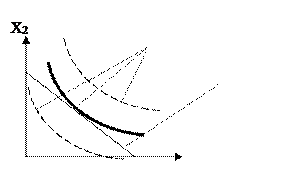
Рис.1.

1.1. Решение задачи потребительского выбора и его свойства .

Набор (х, х) , который является решением задачи потребительского выбора, принято называть оптимальным для потребителя.

Рассмотрим некоторые свойства задачи потребительского выбора. Во-первых, решение задачи (х, х) сохраняется при любом монотонном (т.е. сохраняющем порядок значении) преобразовании функции полезности u ( x ₁ , x ₂ ) . Поскольку значениеu (х, х), было максимальным на всём допустимом множестве, оно остаётся таковым и после монотонного преобразования функции полезности (допустимое множество, определяемое бюджетным ограничением, остаётся неизменным). Таким монотонным преобразованием может быть умножение функции полезности на некоторое положительное число, возведение её в положительную степень, логарифмирование.

Во-вторых, решение задачи потребительского выбора не изменится, если все цены и доход увеличиваются (уменьшаются) в одно и то же число раз λ . (λ>0)

Это равнозначно умножению на положительное число λ обеих частей бюджетного ограниченияp ₁ x ₁ + p ₂ x ₂ ≤ Q , что даёт неравенство, эквивалентное исходному. Поскольку ни цены, ни доход Q не входят в функцию полезности, задача остаётся той же, что и первоначально.

Если на каком-то потребительском наборе ( x ₁ , x ₂ ) бюджетное ограничение p ₁ x ₁ + p ₂ x ₂ ≤ Q будет выполняться в виде строгого неравенства, то мы можем увеличить потребление какого-либо из продуктов и тем самым увеличить функцию полезности. Следовательно, набор (х, х) , максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е.

p ₁ х+ p ₂ х= Q .

Графически это означает, что решение (х, х) задачи потребительского выбора должно лежать на бюджетной прямой, которая проходит через точки пересечения с осями координат, где весь доход тратиться на один продукт: (0, ) и ( ,0) .

Итак, задачу потребительского выбора можно заменить задачей на условный экстремум (ибо решение (х, х) этих двух задач одно и то же):

u ( x ₁ , x ₂ )→ max

при условии p ₁ x ₁ + p ₂ x ₂ = Q .

Для решения этой задачи применим метод Лагранжа. Выписываем функцию Лагранжа

L(x₁ ,x_2, λ )= u(x₁ ,x₂ )+ λ (p₁ x₁ +p₂ x₂ -Q),

находим её частные производные по переменным x ₁ , x ₂ и λ , которые приравниваем к нулю:

L= u+λ p₁ =0,