Реферат: Задача потребительского выбора.Функция потребительского предпочтения Стоуна

Общий случай:

Обозначим минимально необходимое количество благ за А:

1) А<I,

При заданных параметрах а, α, р и I мы определим оптимальный набор (,) и значение функции полезности в этой точке (х1,х2,U ):

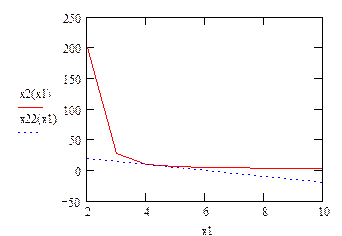
Получим оптимальное значение при потребительском наборе (4,3;8,5), что означает приобретение индивидом 4,3 единицы первого блага и 8,5 единиц второго блага (минимально необходимое количество благ равно 1 и 3 единицам). При данном соотношении достигается максимальное значение функции предпочтения Стоуна – 3,75 единиц.

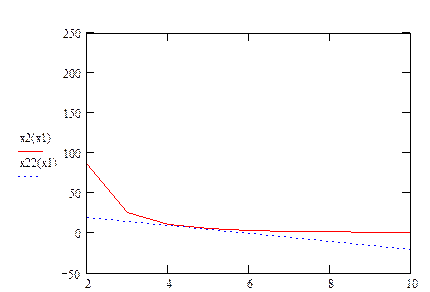
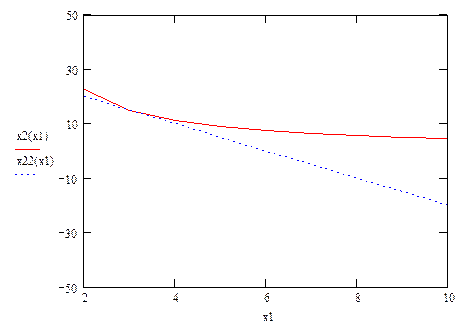
Построим графическую интерпретацию модели Стоуна на основании начальных данных, вычисленного значенияU и теоретических формул для линии безразличия и бюджетной линии:

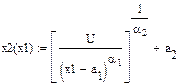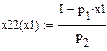2) А=I,

Отсюда следует, что дохода индивида достаточно только для приобретения минимально необходимого ему количества благ. Дальнейшее приобретение благ в соответствии с коэффициентом предпочтения невозможно.

3) А>I,

Из этих расчетов видно, что дохода индивида в данном случае не хватит на приобретение самого необходимого.

Частные случаи:

1)

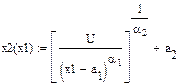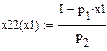При отсутствии минимального необходимого количества благ весь доход (I) используется для приобретения благ в соответствии с коэффициентом предпочтения.

2)

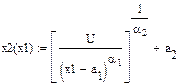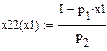В данном случае доход, фактически, делится пополам, так как i=2, и спрос на каждый товар рассчитывается как частное от деления полученной суммы денег на соответствующую ему цену.