Реферат: Задачи линейной алгебры Понятие матрицы Виды матриц Операции с матрицами Решение задач на преобразование

(1.9)

Формула (1.9) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Словесная формулировка этого правила такова: определитель второго порядка, соответствующий матрице (1.8), равен разности произведения элементов, стоящих на главной диагонали этой матрицы, и произведения элементов, стоящих на побочной ее диагонали. Определители второго и более высоких порядков находят широкое применение при решении систем линейных уравнений.

Рассмотрим, как выполняются операции с матрицами в системе MathCad. Простейшие операции матричной алгебры реализованы в MathCad в виде операторов. Написание операторов по смыслу максимально приближено к их математическому действию. Каждый оператор выражается соответствующим символом. Рассмотрим матричные и векторные операции MathCad 2001. Векторы являются частным случаем матриц размерности n x 1, поэтому для них справедливы все те операции, что и для матриц, если ограничения осо­бо не оговорены (например, некоторые операции применимы только к квадратным матрицам n x n ). Какие-то действия допустимы только для векторов (например, скалярное произведение), а какие-то, несмотря на одинако­вое написание, по-разному действуют на векторы и матрицы.

??? ?????? ? ????????? ???????????? ?????? ???????????? ?????????

Рис.1 Панель инструментов Матрицы

Для ввода матрицы:

-введите имя матрицы и знак присваивания (двоеточие)

-щелкните по значку “создать матрицу” в панели “Матрицы”.

-

? ??????????? ??????? ??????? ????? ????? ? ???????? ???????.

-После нажатия кнопки OK открывается поле для ввода элементов матрицы. Для того, чтобы ввести элемент матрицы, установите курсор в отмеченной позиции и введите с клавиатуры число или выражение.

Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно:

-выделить матрицу и щелкнуть в панели по кнопке операции,

-или щелкнуть по кнопке в панели и ввести в помеченной позиции имя матрицы.

Меню “Символы” содержит три операции - транспонирование, инвертирование, определитель .

Это означает, например, что вычислить определитель матрицы можно, выполнив команду Символы/Матрицы/Определитель .

Номер первой строки (и первого столбца) матрицы MathCAD хранит в переменной ORIGIN. По умолчанию отсчет ведется от нуля. В математической записи чаще принято вести отсчет от 1. Для того, чтобы MathCAD вел отсчет номеров строк и столбцов от 1, нужно задать значение переменной ORIGIN:=1.

Функции, предназначенные для работы с задачами линейной алгебры, собраны в разделе “Векторы и матрицы” диалога “вставить функцию” (напоминаем, что он вызывается кнопкой на панели “Стандартные”). Основные из этих функций будут описаны позже.

Транспонирование

Рис.2 Транспонирование матриц

Транспортированием ???????? ????????, ??????????? ??????? ????????????mxn? ??????? ???????????nxm,????? ??????? ???????? ??????? ?????????, ? ?????? ? ?????????. ?????? ???????? ? ???????? ?? ???.2. ???? ??????? ???????????????? (transpose) ?????????????? ? ??????? ?????? ?????????????Matrix (Матрица) ??? ???????? ?????? <Ctrl>+<1>. He ?????????, ??? ??? ??????? ??????? ???????????????? ??????? ?????? ?????????? ?????? ??????? ?????. Напоминание о линиях ввода по отношению к матрицам приведено ранее.

Сложение

?MathCAD ????? ??? ?????????? ???????, ??? ? ???????? ?? ???? ?? ?????. ??? ???? ?????????? ??????????? ??????? <+> ??? <-> ???????????????. ??????? ?????? ????? ?????????? ???????????, ????? ????? ??????? ????????? ?? ??????. ?????? ??????? ????? ???? ?????? ????? ????? ??????????????? ????????? ??????-????????? (?????? ?? ???.3).

Рис.3 Сложение матриц

Рис.4 Сложение матрицы со скаляром

????? ???????? ??????,MathCAD ???????????? ???????? ???????? ??????? ?? ????????? ?????????, ?.?. ?????? (?????? ?? ???.4). ?????? ??????? ?????????????? ??????? ????? ????? ?????????-??????? ???????? ???????? ??????? ? ????????? ????????.

Рис.5 Смена знака матрицы

????????? ????? ????? ??????? ???????????? ????? ????? ???? ?? ?????????. ??? ???? ????? ???????? ???? ???????, ?????????? ?????? ????? ??? ???? ??????, ??? ????? ??????? ?????? (?????? ?? ???.4).

Умножение

При умножении следует помнить, что матрицу размерностиm x n допустимо умножать только на матрицу-размерностиn x p (р может быть любым). В результате получается матрица размерности m х р.

????? ?????? ?????? ?????????, ????? ?????? ??????? ?? ?????????? <*> ??? ??????????????? ??????? ????????????Matrix (Матрица), ????? ?? ??? ??????Dot Product (Умножение) (???.1). ????????? ?????? ???????????? ?? ????????? ??????, ??? ???????? ? ??????? ?? ???6. ?????? ????????? ?????? ????? ???????? ????? ??? ??, ??? ? ? ????????? ??????????.

Рис. 6 Умножение матриц

???????? ????????, ??? ??????? ??????????? ??????? A и B ?????????????????? (??????????? 2?3) ??????? ????????? ???????????????: ????? ?????????? ????? ????????? ????????? ?????? ????????????????, ? ???? ????????? ? ????????? MathCad ?????????? ??????? ??????. ??? ????????? ??????? ?? ??? ?????????, ?????????? ????????? ? ???????????? ????? ????? ?????? ??????? ????? ???????? ?????? ???????.
??? ???? ??????, ??????????? ? ????????? ??????? ?? ???????-?????? ?, ????????, ?????? ?? ??????, ???????? ?? ???. 7. ?? ?????? ?????? ????? ??????? ????????, ??? ???????? ??????? ??? ?????? ??????????? ????????? ?????????No Space (Вместе). ?????? ??? ?? ????? ???????? ????????? ????????? ?? ??? ??????? ??-???????.

Рис.8 Умножение матрицы на скаляр

Рис.7 Умножение вeктopa и строки

?????????? ???????? ?????? ?? ???????? ???????????? ????????? ? ??????? ??????? ?? ????????? ???????? (?????? ?? ???.8). ?????? ????????? ????????? ??? ??, ??? ? ? ?????? ????????? ???? ??????. ?? ?????? ????? ????????? ????? ??????? ??????? m x n .

Определитель квадратной матрицы

Определитель (Determinant) матрицы обозначается стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопкуDeterminant (Определитель) на панели инструментов Matrix (Матрица) (рис. 1) или набрать на клавиатуре <|> (нажав клавиши < Shift >+<\> ). В результате любого из этих действий появляется местозаполнитель, в который следует поместить матрицу. Чтобы вычислить определи­ть уже введенной матрицы, нужно выполнить следующие действия:

1. Переместить курсор в документе таким образом, чтобы поместить матри­цу между линиями ввода (напоминаем, что линии ввода — это верти­кальный и горизон-тальный отрезки синего цвета, образующие уголок, указывающий на текущую область редактирования).

2. Ввести оператор нахождения определителя матрицы.

3. Ввести знак равенства, чтобы вычислить определитель.

Рис.9 Поиск определителя квадратной матрицы

????????? ?????????? ???????????? ???????? ? ??????? ?? ???. 9.

Модуль вектора

Модуль вектора (vectormagnitude) ???????????? ??? ?? ????????, ??? ? ???????????? ???????. ?? ???????????, ?????? ??????? ????? ??????????? ????? ?? ????? ????????? ??? ????????? (?????? ?? ???.10).

Рис.10 Поиск модуля вектора

Скалярное произведение векторов

Скалярное произведение векторов (vectorinnerproduct) ???????????? ??? ???????, ?????? ????? ???????? ???????????? ??????????????? ?????????. ??????? ?????? ????? ?????????? ???????????, ????????? ???????????? ????? ?? ?? ???????????. ????????? ???????????? ???? ???????? u ?v ????? u · v = | u | · | v | · cos j , ??? j ? ???? ????? ?????????. ???? ??????? ????????????, ?? ????????? ???????????? ????? ????. ???????????? ????????? ???????????? ??? ?? ???????? ????????? (?????? ?? ???.11). ??? ??????????? ??????????? ???????????? ???????????? ????? ????? ???????? ????????????? ?????????? ?????????.

Рис.11 Скалярное произведение векторов

Никогда не применяйте для обозначения скалярного произведения символ который является общеупотребительным символом векторного произведения.

? ????????????? ???????????? ????????? (????? ????) ????????. ??-??????? ????????????? ?????? ????????? ???????? ????????? ?????????. ??????? ?????? ????????? ??. ? ???????? ?? ???.12.

Рис.12 Особенности скалярного произведения векторов

Векторное произведение

Рис.13 Векторное произведение векторов

Векторное произведение ( cross product ) ???? ???????? u ?v ? ????? a ????? ???? ????? ??????? ? ???????| u | · | v | · sin a , ???????????? ??????????????? ???????? ???????? u ? v . ?????????? ????????? ???????????? ???????? х, ??????? ????? ?????? ???????? ??????Cross Product (Векторное произвение) ? ??????Matrix (Матрица) ??? ?????????? ??????< Ctrl >+<8>. ?????? ???????? ?? ???.13.

Задание 1.

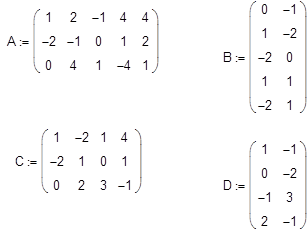????????? ??????? 2*A*B-3*C*D, ???:
?????:
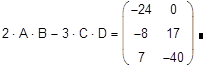