Реферат: Задачи Пятого Турнира Юных Математиков

Аналогично,
![]() и
и ![]() .
.
Тогда 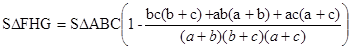
Упростив это выражение, получаем ![]() .
.
Теперь, из неравенства Коши (![]() ) Þ
) Þ![]() .
.
Итак,отношение площади треугольника![]() FHG (по условию - Sl ), вершины которого – основания биссектрис данного треугольника, к площади треугольника
FHG (по условию - Sl ), вершины которого – основания биссектрис данного треугольника, к площади треугольника ![]() АВС -
АВС - ![]() .
.
Этап 3 : Найдем отношение площади треугольника, образованного основаниями медиан, к данному треугольнику ![]() ABC.
ABC.
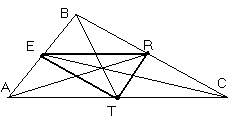 Проведем из вершин
Проведем из вершин ![]() АВС медианы, пересекающие стороны АВ, ВС и АС соответственно в точках E, R и T.
АВС медианы, пересекающие стороны АВ, ВС и АС соответственно в точках E, R и T.
Рассмотрим AERT.
RT, по свойству средней линии равен половине АЕ и АЕ7RT.
ER=AT и ER7AT по этим же признакам ÞAERT – параллелограмм.
Значит ÐEAT=ÐERT (*) – по свойству параллелограмма.
Аналогичным образом рассмотрим параллелограммы ERCT, BETR. Из них ÞÐRET = ÐRCT, ÐRBE = ÐETR (**).
Из (*) и (**) Þ![]() ERT подобен
ERT подобен ![]() АВС при
АВС при ![]() (по свойству средней линии). По свойству «площади подобных фигур относятся как квадраты коэффициентов подобия»,
(по свойству средней линии). По свойству «площади подобных фигур относятся как квадраты коэффициентов подобия», ![]() .
.
Итак, отношение площади треугольника (по условию SK ), образованного основаниями медиан, к площади данного треугольника АВС - ![]() .
.
Этап 4 :докажем, что ![]() .
.
В процессе решения задачи данный этап был разрешен, но найденное решение оказалось крайне не рациональное и очень объемное, поэтому здесь не приведено.
Значит, действительно, площадь треугольника, образованного основаниями медиан больше площади треугольника, образованного основаниями биссектрис, который больше площади треугольника, образованного точками касания вписанной окружности. ЧТД.
Задача 1 Финального тура
Условие: Решить уравнение xy2 + xy + x2 – 2y – 1 = 0 в целых числах.
Решение
Представим исходное уравнение в виде:
![]()
Из этого следует, что х – делитель 2у+1. Введем замену: 2у+1 = kx, где kÎZ. Тогда
![]() Т.к. ищем решения в целых числах, из этого равенства видно, что k – число нечетное.
Т.к. ищем решения в целых числах, из этого равенства видно, что k – число нечетное.
![]()
Подставим значения в преобразованное уравнение.
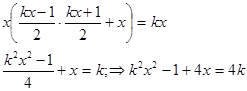
Введем замену: х1 = -х. Тогда полученное уравнение примет вид ![]() .
.
Решим данное уравнение относительно х1 (очевидно, что ![]() ).
).
1. Рассмотрим случай, когда k = 1. ![]()
Отсюда, х = 1 или х = = -5, тогда y = 0 или у = -3;
Ответ: (1;0), (0;-3);
2. Рассмотрим случай, когда k = -1. ![]()
Отсюда, х = -1 или х = = -3, тогда у = 0 или у = 1;
Ответ: (-1;0), (-3;1);
3. Рассмотрим случай, когда k = 3. ![]() Отсюда у = -14.
Отсюда у = -14.
Ответ: (-9;-14)
4. Рассмотрим случай, когда k = -3. ![]() - нет решений в области целых чисел.
- нет решений в области целых чисел.
Итак, в результате вышеописанных вычислений были найдены следующие решения: (1;0), (0;-3), (-1;0), (-3;1), (-9;-14).
C умма производных
Условие: Пусть
![]() .
.