Реферат: Задачі сигналів та критерії оптимальності рішень
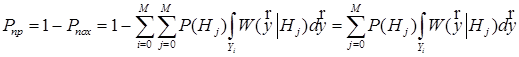 . (4)
. (4)
Показник апостеріорної ймовірності гіпотези. Матриця втрат ![]() – це додаткова апріорна інформація, що може бути не задана. У цьому разі раціонально вибрати критерій, в якому вона не фігурує. Це може бути апостеріорна ймовірність гіпотези
– це додаткова апріорна інформація, що може бути не задана. У цьому разі раціонально вибрати критерій, в якому вона не фігурує. Це може бути апостеріорна ймовірність гіпотези ![]() , що обчислюється за формулою Байєса:
, що обчислюється за формулою Байєса:
 . (5)
. (5)
Використовують й інші показники якості. Досить часто (особливо в задачах оцінювання параметрів) закритерій якості приймають саму функцію правдоподібності.
Розглянуті показники якості рішення використовують для формулювання критеріїв оптимальності рішень при розв’язанні задач обробки сигналів.
3. К ритерії оптимальності рішень у задачі перевірки гіпотез
Розглянемо критерії оптимальності рішень при вирішенні задач перевірки гіпотез.
Байєсівський критерій оптимальності використовує середній ризик (2) і вимагає його мінімізації (у загальному випадку забезпечення нижньої границі):
 . (6)
. (6)
Рішення – це гіпотеза ![]() , що забезпечує мінімум середнього ризику. Останній шукається у множині
, що забезпечує мінімум середнього ризику. Останній шукається у множині ![]() відображень простору спостережень
відображень простору спостережень ![]() у простір рішень
у простір рішень ![]() . Нагадаємо, що аргумент функції правдоподібності – це значення параметра
. Нагадаємо, що аргумент функції правдоподібності – це значення параметра ![]() (або номер гіпотези). Тому зручно (6) записувати також у вигляді
(або номер гіпотези). Тому зручно (6) записувати також у вигляді
![]() . (7)
. (7)
Критерій мінімуму середньої ймовірності похибки (критерій Зігерта-Котельникова або критерій ідеального спостерігача). У цьому разі використовується показник якості рішення (3). Цей критерій оптимальності вимагає мінімізації величини середньої ймовірності похибки:
 , (8)
, (8)
або
![]() . (8а)
. (8а)
Критерій називають також критерієм „ідеального спостерігача”, тому що можна уявити собі, що деякий спостерігач задає вагову матрицю ![]() так, що вона завжди нульова
так, що вона завжди нульова ![]() , коли приймається правильне рішення. А коли виникає похибка,він не цікавиться тим, як саме вона виникла, і завжди задає однаковий вагомий коефіцієнт
, коли приймається правильне рішення. А коли виникає похибка,він не цікавиться тим, як саме вона виникла, і завжди задає однаковий вагомий коефіцієнт ![]() .
.
Іноді зручніше використовувати замість ![]() максимум імовірності правильного рішення (4):
максимум імовірності правильного рішення (4):
 . (9)
. (9)
Критерій максимуму апостеріорної ймовірності. Згідно з показником якості (5) критерій оптимальності рішення задається так: серед гіпотез ![]() вибирається такий номер „
вибирається такий номер „![]() ”, що забезпечується максимум у (5):
”, що забезпечується максимум у (5):
 . (10)
. (10)
Мінімаксний критерій оптимальності . Введені вище критерії по суті вимагали знання розподілу ![]() переданого сигналу, що дає змогу ввести ймовірності гіпотез
переданого сигналу, що дає змогу ввести ймовірності гіпотез ![]() . Коли розподіл
. Коли розподіл ![]() невідомий, можна врахувати найгірший випадок – мінімізувати середній ризик в умовах найгіршого (з точки зору величини ризику) розподілу:
невідомий, можна врахувати найгірший випадок – мінімізувати середній ризик в умовах найгіршого (з точки зору величини ризику) розподілу:
 . (11)
. (11)
У теорії статистичних рішень доводиться, що рішення буде таке саме, якщо використовувати умовні ризики

та вимагати, щоб рішення шукалось за умови
 . (11а)
. (11а)
Мінімаксний критерій приводить до байєсівського рішення в умовах найгіршого розподілу параметра (переданого сигналу).
Критерій оптимальності Неймана-Пірсона. Спинимося детальніше на ілюстрованому прикладі приймання сигналів амплітудної маніпуляції. Тут задається лише дві гіпотези. Гіпотезу ![]() називають основною, а
називають основною, а ![]() – альтернативною. Ставиться задача перевірки гіпотези
– альтернативною. Ставиться задача перевірки гіпотези ![]() проти альтернативи
проти альтернативи ![]() . Часто гіпотези несиметричні і зручно основну увагу приділити одній з них. Саме таку гіпотезу у математичній статистиці називають основною і позначають
. Часто гіпотези несиметричні і зручно основну увагу приділити одній з них. Саме таку гіпотезу у математичній статистиці називають основною і позначають ![]() .
.
У задачі перевірки гіпотези ![]() проти альтернативи
проти альтернативи ![]() мають місце дві похибки – умовні ймовірності:
мають місце дві похибки – умовні ймовірності: