Реферат: Защита информации цифровая подпись

|k _V |=2|X |=2n .

Алгоритм Sig выработки цифровой подписи для бита t (t О{0,1}) заключается просто в выборе соответствующей половины из пары, составляющей секретный ключ подписи:

s = S (t ) = k _t .

Алгоритм Ver проверки подписи состоит в проверке уравнения E_kt (X _t )=C _t , которое, очевидно, должно выполняться для нашего t . Получателю известны все используемые при этом величины.

Таким образом, функция проверки подписи будет следующей:

.

Покажем, что данная схема работоспособна, для чего проверим выполнение необходимых свойств схемы цифровой подписи:

1. Невозможность подписать бит t , если неизвестен ключ подписи. Действительно, для выполнения этого злоумышленнику потребовалось бы решить уравнение E _s (X _t )=C _t относительно s , что эквивалентно определению ключа для известных блоков шифрованного и соответствующего ему открытого текста, что вычислительно невозможно в силу использования стойкого шифра.

2. Невозможность подобрать другое значение бита t , которое подходило бы под заданную подпись, очевидна: число возможных значений бита всего два и вероятность выполнения двух следующих условий одновременно пренебрежимо мала в просто в силу использования криптостойкого алгоритма:

E _s (X ₀ )=C ₀ ,
E _s (X ₁ )=C ₁ .

Таким образом, предложенная Диффи и Хеллманом схема цифровой подписи на основе классического блочного шифра обладает такой же стойкостью, что и лежащий в ее основе блочный шифр, и при этом весьма проста. Однако, у нее есть два существенных недостатка.

Первый недостаток заключается в том, что данная схема позволяет подписать лишь один бит информации. В блоке большего размера придется отдельно подписывать каждый бит, поэтому даже с учетом хэширования сообщения все компоненты подписи – секретный ключ, проверочная комбинация и собственно подпись получаются довольно большими по размеру и более чем на два порядка превосходят размер подписываемого блока. Предположим, что в схеме используется криптографический алгоритм E_K с размером блока и ключа, соответственно n и n_K . Предположим также, что используется функция хэширования с размером выходного блока n_H . Тогда размеры основных рабочих блоков будут следующими:

размер ключа подписи: n_kS =2n_H Чn_K .

размер ключа проверки подписи: n _С =2n_H n .

размер подписи: n_S =n_H Ч n_K .

Если, например, в качестве основы в данной схеме будет использован шифр ГОСТ 28147–89 с размером блока n =64 бита и размером ключа n_K =256 бит, и для выработки хэш–блоков будет использован тот же самый шифр в режиме выработки имитовставки, что даст размер хэш–блока n_H =64 то размеры рабочих блоков будут следующими:

размер ключа подписи: n_kS =2n_H Чn_K =2Ч 64Ч 256бит=4096 байт;

размер ключа проверки подписи: n _С =2n_H n = 2Ч 64Ч 64 бит = 1024 байта.

размер подписи: n_S =n_H Ч n_K = 64Ч 256 бит = 2048 байт.

Второй недостаток данной схемы, быть может, менее заметен, но столь же серьезен. Дело в том, что пара ключей выработки подписи и проверки подписи могут быть использованы только один раз. Действительно, выполнение процедуры подписи бита сообщения приводит к раскрытию половины секретного ключа, после чего он уже не является полностью секретным и не может быть использован повторно. Поэтому для каждого подписываемого сообщения необходим свой комплект ключей подписи и проверки. Это практически исключает возможность использования рассмотренной схемы Диффи–Хеллмана в первоначально предложенном варианте в реальных системах ЭЦП.

Однако, несколько лет назад Березин и Дорошкевич предложили модификацию схемы Диффи–Хеллмана, фактически устраняющую ее недостатки.

Центральным в этом подходе является алгоритм «односторонней криптографической прокрутки», который в некотором роде может служить аналогом операции возведения в степень. Как обычно, предположим, что в нашем распоряжении имеется криптографический алгоритм E_K с размером блока данных и ключа соответственно n и n_K бит, причем n Јn_K .

Пусть в нашем распоряжении также имеется некоторая функция отображения n –битовых блоков данных в n _K –битовые Y =P _{n ® nK} (X ), |X |=n , |Y |=n_K . Определим рекурсивную функцию R_k «односторонней прокрутки» блока данных T размером n бит k раз (k і0) при помощи следующей формулы:

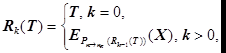
где X – произвольный несекретный n -битовый блок данных, являющийся параметром процедуры прокрутки.

По своей идее функция односторонней прокрутки чрезвычайно проста, надо всего лишь нужное количество раз (k ) выполнить следующие действия: расширить n -битовый блок данных T до размера ключа использованного алгоритма шифрования (n_K ), на полученном расширенном блоке как на ключе зашифровать блок данных X , результат зашифрования занести на место исходного блока данных (T ). По определению операция R_k (T ) обладает двумя важными для нас свойствами:

1. Аддитивность и коммутативность по числу прокручиваний:

R_{k +k '} (T )=R_{k '} (R_k (T )) = R_k (R_{k '} (T )).

2. Односторонность или необратимость прокрутки: если известно только некоторое значение функции R_k (T ), то вычислительно невозможно найти значение R_{k '} (T ) для любого k ' <k – если бы это было возможно, в нашем распоряжении был бы способ определить ключ шифрования по известному входному и выходному блоку алгоритма E_K . что противоречит предположению о стойкости шифра.