Реферат: Знаходження похідної функції

3) .

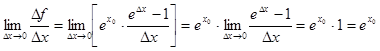Таким чином, похідна функції е^х дорівнює самій функції:

Знайдемо похідну функції , скориставшись основною логарифмічною тотожністю та правилом знаходження похідної складеної функції:

.

Отже,

Похідна показникової функції дорівнює добутку цієї функції на натуральний логарифм її основи.

Приклад 1. Знайдіть похідну функцій:

а) у = 5^х ; б) у = е^3-2х ; в) ; г) .

Розв’язання

а) ;

б) ;

в) ;

г) .

Виконання вправ.

№ 2 (2, 4, 6, 8, 10, 12), №2 (20, 22, 24, 26, 28, 30) із підручника (розділ Х).

ІІІ. Сприймання і усвідомлення матеріалу про похідну логарифмічної функції

Розглянемо функцію . За основною логарифмічною тотожністю: для всіх додатних х.

Диференціюючи обидві частини цієї рівності, одержимо: , або .

Звідси .

Отже,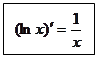

Знайдемо похідну функції . Так як , то

.

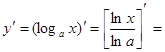
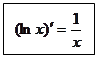
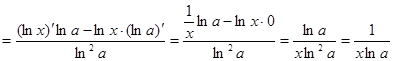Отже,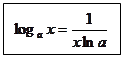

Приклад 1. Знайдіть похідну функцій:

а) ; б) ;